Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 10

СТЬЮДРАСПОБР(ймовірність; ступені_вільності) – повертає значення х_α для двостороннього розподілу Стьюдента, що є розв’язком рівняння  .

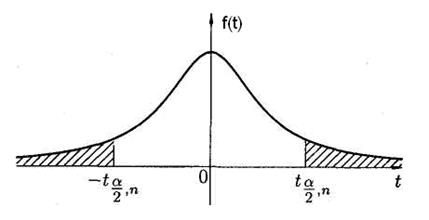
Рисунок 3.8 – Геометрична  інтерпретація двостороннього розподілу Стьюдента

Якщо потрібно розв’язати рівняння , необхідно задати СТЬЮДРАСПОБР (1-g ; ступені_вільності).

3.4 F-розподіл (розподіл Фішера)

Важливе використання у статистиці має випадкова величина

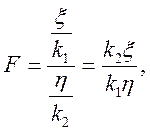
де x – випадкова величина, що розподілена за законом c² з k₁ ступенями вільності, а h – випадкова величина, що розподілена за законом c² з k₂ ступенями вільності.

Випадкова величина F розподілена за законом розподілу Фішера з k₁ і k₂ ступенями вільності. При заданих числах k₁ і k₂ та за ймовірністю α за таблицею визначається значення F _α, таке, що

P(F > F _α) = α.

Звичайно таблиці складаються для значень α, що дорівнюють 0,05 або 0,01, а іноді для обох цих значень.

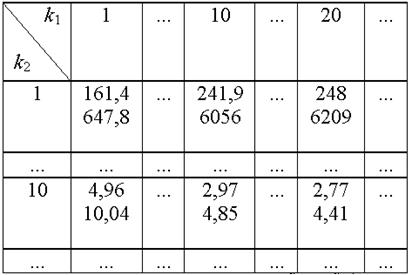
У цій таблиці у верхній частині кожної клітинки дається значення F _α при α = 0,05 , а в нижній частині – при α = 0,01.

Рисунок 3.9 – Геометрична інтерпретація розподілу Фішера

В Excelдля роботи з розподілом Фішера можна використовувати такі функції :

FРАСП(F_α; ступені_вільності1; ступені_вільності2).

Повертає ймовірність α, що є розв’язком рівняння .  Цю функцію можна використовувати, щоб визначити, чи мають дві множини даних різні ступені розкиду результатів.

FРАСПОБР (ймовірність; ступені_вільності1; ступені_вільності2) – обчислюється значення F_α, що є розв’язком рівняння .

Питання і завдання до розділу 3

1 Нормальний закон розподілу та його основні параметри.

2 Як впливає зміна параметрів m та σ на форму кривої Гаусса?

3 Стандартний нормальний закон розподілу та його основні параметри.

4 Як обчислюється ймовірність попадання випадкової величини X ~ N(m, σ) на заданий проміжок (x₁;x₂)?

5 Формула для обчислення ймовірності заданого відхилення від математичного сподівання.

6 Правило трьох сигм. Як його застосовують на практиці?

7 Функції Excel для роботи з нормальним розподілом.

8 Що характеризує асиметрія?

9 Що характеризує ексцес?

10 Дайте визначення розподілу Пірсона.  Функції Excel для роботи з цим розподілом.

11 Дайте визначення розподілу Стьюдента.  Функції Excel для роботи з цим розподілом.

12 Дайте визначення розподілу Фішера.  Функції Excel для роботи з цим розподілом.

Лабораторна робота

Тема. Нормальний закон розподілу

За допомогою можливостей Excel знайти ймовірність попадання у заданий інтервал (α,β)  нормально розподіленої випадкової величини Х , якщо відомі її математичне сподівання  М і середнє квадратичне  відхилення   σ.

Знайти ймовірність відхилення випадкової величини від математичного сподівання не більше ніж на δ.

Побудувати :

ü  функцію щільності розподілу;

ü  функцію розподілу.

 Нанести на графік значення математичного сподівання та інтервали (М±σ), (М±3σ).

Варіант	α	β	М	σ	δ
1	2	13	10	4	6
2	5	14	9	5	4
3	6	9	8	1	2
4	3	10	7	2	4
5	2	11	6	3	5

Вказівка. Для розрахунку інтервалу можливих значень Х використайте правило трьох сигм.

4 ВИБІРКОВИЙ МЕТОД

4.1 Теорема Чебишева

Якщо  – попарно незалежні випадкові величини, причому дисперсії їх рівномірно обмежені (тобто не перевищують деяке число С), то яким би малим не було , ймовірність нерівності

 

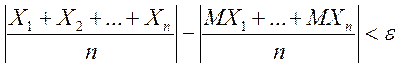
буде  як завгодно близька до 1, якщо число випадкових величин досить велике.

.

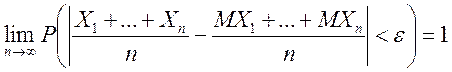Якщо MX₁=…=MX_n=a, .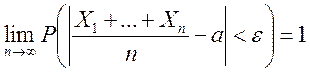

Сутність: середнє арифметичне досить великого числа незалежних випадкових величин  втрачає характер випадкової величини.

Значення: на цій теоремі базується широко застосовуваний у статистиці вибірковий метод, суть якого полягає в тому, що за порівняно невеликою вибіркою судять про всю сукупність досліджуваних об'єктів.