Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 31

	Столбец 1	Столбец 2	Столбец 3
Столбец 1	1
Столбец 2	-0,565031	1
Столбец 3	0,9872039	-0,6049951	1

Будуємо кореляційну матрицю Q

1	-0,565031	0,9872039
-0,56503	1	-0,6049951
0,987204	-0,604995	1

2 Розрахунок оцінок часткових коефіцієнтів кореляції.

Знаходимо обернену матрицю Z за допомогою функції EXCEL МОБР(<діапазон>).

42,03319	-2,13634	-42,7878
-2,13634	1,685914	3,128971
-42,7878	3,128971	45,1333

Оцінки часткових коефіцієнтів кореляції визначаються за формулою (6.7).

Одержуємо такі значення:

r12,y=	0,253779237
r1y,2=	0,982370424
r2y,1=	-0,35870321

Варто мати на увазі, що частковий коефіцієнт кореляції може різко відрізнятися від відповідного парного коефіцієнта і навіть мати протилежний знак. Кожний із часткових коефіцієнтів може дорівнювати нулю, у той час як значення відповідних парних  коефіцієнтів буде відмінне від нуля.

У даному прикладі r_12,y=0,25378, а r₁₂=-0,565, тобто чистий зв'язок між обсягом валової продукції (X₁) і продуктивністю праці (X₂) незначний. Зв'язок обсягу валової продукції (X₁) і собівартості товарної продукції (Y): r_1y=0,987, r_1y,2=0,982 сильний. У випадку незалежності величин частковий і парний коефіцієнти кореляції дорівнюють нулю.

3 Розрахунок оцінок множинних коефіцієнтів кореляції й детермінації. Оцінки множинних коефіцієнтів кореляції та  детермінації розраховуються за формулами:

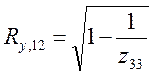=0,989,

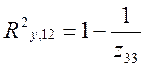=0,978.

Значення множинних коефіцієнтів кореляції  й детермінації близькі до 1, що свідчить про наявність сильної лінійної залежності Yвід X₁ і X₂, тобто собівартість дійсно залежить від обсягу валової продукції і продуктивності праці.

Питання і завдання до розділу 6

1  Дайте визначення функціонального і кореляційного зв’язку. Як проявляється кореляційний зв’язок?

2  Які Ви знаєте форми кореляційного зв’язку? Наведіть приклади.

3  Які задачі розв’язуються за допомогою кореляційного аналізу?

4  Назвіть основні етапи кореляційного аналізу і розкрийте їх суть.

5  Які показники використовують для вимірювання тісноти зв’язку між ознаками при лінійній залежності?

6  Що характеризують коефіцієнт кореляції і коефіцієнт детермінації?

7  Про що свідчить знак лінійного коефіцієнта кореляції?

8  Дайте визначення множинної кореляції.

9  Який зміст коефіцієнтів парної і часткової кореляції?

Лабораторна робота

Тема. Багатофакторний  кореляційний аналіз

Завдання. За вибірковими даними, наведеними в табл. 6.3 і табл. 6.5, дослідити кореляційну залежність результативної ознаки від показників виробничо-господарської діяльності підприємств, а також кореляційну залежність між факторними ознаками.

1  Обчислити коефіцієнти коваріації та  кореляції 3 способами:

ü  за формулами;

ü  з використанням функцій КОВАР() і КОРРЕЛ();

ü  з використанням пакета аналізу (Ковариация, Корреляция).

2  Побудувати матриці парних і часткових коефіцієнтів кореляції.

3  Знайти множинні коефіцієнти кореляції і детермінації.

4  Перевірити значущість парних, часткових та множинних коефіцієнтів кореляції.

Зробити висновки про типи зв’язку та його сили для досліджуваних факторів. Провести змістовний економічний аналіз отриманих результатів.

Таблиця 6.3 – Варіанти завдань

Номер варіанта	Результативна ознака	Факторні ознаки	Номер варіанта	Результативна ознака	Факторні ознаки
1	y1	x1,x3	6	y2	x1,x2
2	y2	x1,x5	7	y2	x5,x9
3	y2	x1,x7	8	y3	x8,x10
4	y2	x1,x10	9	y3	x3,x6
5	y1	x3,x4	10	y1	х1,x6