Информатика и выч. техника \ Анализ данных

Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 29

2 Наявність статистичного зв'язку необов'язково означає наявність фізичного зв'язку (причинно-наслідковий зв'язок).

Причиною може бути те, що випадкові величини X і Y обидві залежать від змінної Z. У цьому випадку при проведенні кореляційного аналізу ми бачимо зв'язок, який у фізичному змісті відсутній.

У Стокгольмі в 60-ті роки ХХ ст. був обчислений  коефіцієнт кореляції між кількістю лелек, що прилітають, і кількістю дітей, що народжуються. Він виявився близьким до 1. Але обидва ці явища залежать від кількості домогосподарств.

У США встановили наявність позитивного зв'язку між кількістю церков і барів (чим більше церков, тим більше барів). Насправді ці величини залежать від розміру міста.

3 З наявності кореляційного зв'язку, що відбиває дійсно існуючий фізичний зв'язок, варто робити правильні висновки. Наприклад, з наявності зворотного зв'язку між температурою повітря й кількістю палива для обігріву приміщення зовсім не випливає, що чим більше топити, тим холодніше буде на вулиці.

6.1.2 Значущість коефіцієнта кореляції

Щоб перевірити, чи значуще коефіцієнт кореляції відрізняється від 0, використовують критеріальне значення

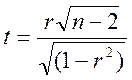,                                    (6.3)

 яке є розподілом Стьюдента з k=N-2 ступенями вільності. При заданому рівні значущості  критичне значення tкр знаходять із рівняння P(|t|>tкр)=.

Якщо , то rxy не значуще відрізняється від 0, і приймають гіпотезу про відсутність лінійного кореляційного зв'язку між змінними.

Якщо , то rxy  значуще відрізняється від 0, і приймають гіпотезу про наявність лінійного кореляційного зв'язку між змінними.

Залежно від значення  розрізняють такі види зв'язку:

0 – 0,3 – слабкий зв'язок; 0,3 – 0,7 – середній зв'язок; 0,7 – 1 – сильний зв'язок.

Приклад. Проаналізувати зв'язок між балом ураження яблунь шкідниками та їх урожайністю. Дані наведені в таблиці 6.1.

Таблиця 6.1 – Значення балу ураження та урожайності яблунь

X

Y

XY

4

10

40

1

15

15

2

20

40

3

10

30

5

5

25

5

10

50

2

25

50

1

20

20

3

15

45

4

15

60

=3

=14,5

37,5

σх =1,41421

σy=5,678908

 =СТАНДОТКЛОНП()

r xy=-0,747

,

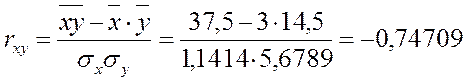 коррел(<діапазон>)= –0,74709.

Перевіряємо значущість коефіцієнта кореляції з рівнем значущості α=0,05.

 ,

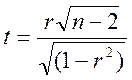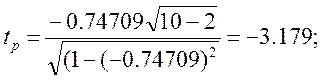
tкр= СТЬЮДРАСПОБР(0,05; 10-2)=2,306,   

/tр/ > tкр – отже, коефіцієнт кореляції є статистично значущим.

Висновок: між балом ураження шкідниками й урожайністю  яблунь існує сильний зворотний лінійний зв'язок.

6.2 Поняття про багатовимірний кореляційний аналіз

Основні поняття кореляційного аналізу, введені для двовимірної моделі, можна поширити на багатовимірний випадок. Однак, якщо при вивченні взаємозв'язків за двовимірною моделлю ми обмежувалися розглядом парних коефіцієнтів кореляції, то для багатовимірних моделей цього недостатньо. Різноманіття зв'язків між змінними знаходить висвітлення в часткових  і множинних коефіцієнтах кореляції.

Нехай є багатовимірна нормальна сукупність із m ознаками X1, X2, …, Xm... У цьому випадку взаємозалежність між ознаками можна описати за допомогою кореляційної матриці. Під кореляційною матрицею будемо розуміти матрицю, складену з парних коефіцієнтів кореляції. Оцінкою парного коефіцієнта кореляції є вибірковий парний коефіцієнт кореляції

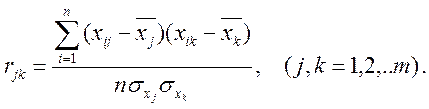                                               (6.4)

Якщо знайдені вибіркові коефіцієнти кореляції, то можна одержати оцінену кореляційну матрицю

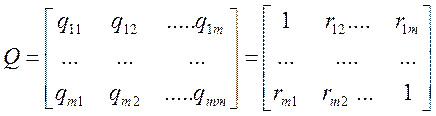.         (6.5)

Ця матриця симетрична.

6.2.1 Часткова кореляція

Коефіцієнти часткової кореляції також характеризують лінійні зв'язки ознак, але при цьому до уваги береться чистий зв'язок пари ознак. Часткові коефіцієнти кореляції характеризують тісноту зв'язку між результатом і відповідним фактором при усуненні впливу інших факторів.

Скачать файл