Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 26

,

 – однобічна (лівостороння) критична точка. = – .

Якщо _р>–, приймаємо H₀ .

Якщо  _р<–, приймаємо H₁ .

Приклад. Вимірювали рівень гемоглобіну в групі пацієнтів до і після лікування. Визначити, чи було лікування ефективним, і чи відповідає нормі 120 рівень гемоглобіну у пацієнтів до і після лікування. Рівень значущості a=0,05.

До лікування	Після лікування
90	100
130	130
100	140
80	90
110	120
130	150
90	110
90	110
60	70
60	80

Перевіряємо, чи вплинуло лікування на рівень гемоглобіну. Для цього перевіряємо рівність середніх для пов’язаних вибірок.

Висуваємо гіпотези:

 H ₀:  _{після лікування} =  _{до лікування}

H ₁: _{після лікування} >  _{до лікування}

Пакет Анализ данных – Парный двухвыборочный t-тест для средних .

Отримаємо таблицю

Парный двухвыборочный t-тест для средних
	Переменная 1	Переменная 2
Среднее	94	110
Дисперсия	604,444444	666,6666667
Наблюдения	10	10
Корреляция Пирсона	0,91018205
Гипотетическая разность средних	0
df	9
t-статистика	-4,7067872
P(T<=t) одностороннее	0,00055476
t критическое одностороннее	2,26215889
P(T<=t) двустороннее	0,00110952
t критическое двустороннее	2,68501026

| t-статистика | > t критическое одностороннее, отже, лікування вплинуло на рівень гемоглобіну.

Перевіримо, чи відповідає нормі цей показник до і після лікування. Для цього обчислимо

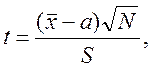
t_р1 – до лікування,         _{до лікування}=94,

;

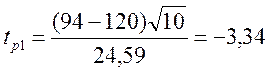t_р2 – після лікування, _{після лікування}=110,

.

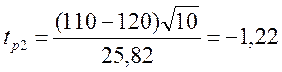Критичне значення обчислюємо за допомогою функції Excel

t_кр = СТЮДРАСПОБР(0,05; 9)= 2,262.

|t _{р до лікування} | > t _кр =>   показник гемоглобіну до лікування не задовольняє нормі.

|t _{р після лікування} | < t _кр  =>    показник гемоглобіну після лікування  задовольняє нормі.

Питання і завдання до розділу 5

1 Які гіпотези називають статистичними?

2 Дайте визначення статистичного критерію.

3 Які гіпотези називають основною та альтернативною?

4 Який зміст рівня значущості α?

5 Від чого залежить вигляд критичної області?

6 Дайте визначення критичної точки.

7 Помилки першого та другого роду. Потужність критерію.

8 Вказати порядок дій при перевірці гіпотез.

9 Критерій для перевірки гіпотези про закон розподілу.

10 Критерій для перевірки гіпотез про рівність дисперсій двох нормальних сукупностей. Можливості Excel.

11 Критерії для перевірки гіпотез про рівність середніх двох нормальних сукупностей. Можливості Excel.

12  Група з 10 школярів протягом літніх канікул перебувала у спортивному таборі. До і після сезону у них визначали місткість легенів (у мілілітрах). За результатами вимірювань необхідно було визначити, чи істотно змінився цей показник під впливом інтенсивних фізичних вправ.

До експерименту	3400	3600	3000	3500	2900	3100	3200	3400	3200	3400
Після експерименту	3800	3700	3300	3600	3100	3200	3200	3300	3500	3600

13 Щоб порівняти відбивну здатність двох видів фарби, проводили такий експеримент: з 10 вибраних  навмання пробних зразків п’ять пофарбували однією фарбою, а решту - іншою. Одержані за допомогою оптичного приладу результати вимірювань наведено нижче.

Фарба Ф	195	150	205	120	160
Фарба В	200	115	220	185	170