Информатика и выч. техника \ Анализ данных

Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 19

Оскільки=42,37, S=0,94, нормальний закон розподілу для нашої вибірки можна записати у вигляді  N(42,37; 0,94).

Обчислення зручно оформити у вигляді  таблиці 5.1.

Таблиця 5.1 – Перевірка гіпотези про закон розподілу

Інтервал

Ки-ше-ні

Середини інтервалів

ni

F(X)

Pi

n’i

cнабл2

Xi

(Xi- Xi-1)/2

Емпіричні частоти

НОРМРАСП(Xi, xср, S,1)

F(Xi)-F(Xi-1)

Теоретичні частоти

NPi

(-∞;40]

40

39,5

0

0,0058

(40;41]

41

40,5

20

0,0724

0,066

24,92

0,97

(41;42]

42

41,5

112

0,3469

0,274

102,63

0,85

(42;43]

43

42,5

154

0,7486

0,401

150,23

0,09

(43;44]

44

43,5

73

0,958

0,209

78,50

0,38

(44;46]

46

45

15

0,999

0,0413

15,48

0,015

Сума

374

c2 р  =

2,32

  

c=ХИ2ОБР(0,01;2)=

9,21

  

Для розглянутого прикладу c2 р = 2,32.

c = Хи2Обр(0,01; 2) = 9,210351(K = 5 – 1 – 2 = 2).

Оскільки  c2 р<  c, гіпотеза про нормальний закон  розподілу  N(20,27; 1,96) приймається з рівнем значущості 0,01.

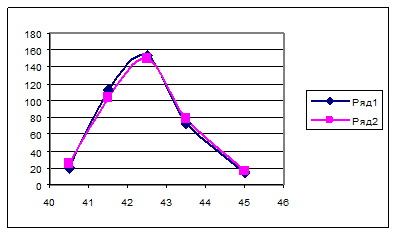
Будуємо діаграму теоретичних та емпіричних частот, відкладаємо відповідні значення частот на серединах інтервалів.

5.2 Поняття про параметричну, непараметричну і робастну статистику

При перевірці будь-якої гіпотези необхідно спиратися на якусь сукупність припущень, з яких і виводяться формули, необхідні для цієї перевірки. При цьому серед інших завжди наявні припущення про закон розподілу. 

Невиконання цих передумов робить некоректним застосування відповідних методів.

Параметричні методи припускають конкретний розподіл. Ці методи строго обґрунтовані і добре вивчені. Проблема в тому, що в багатьох практичних задачах передумови нормальності розподілу не виконуються.

Робастні методи припускають конкретний розподіл, але допускають відхилення від нього. Форма і величина відхилень залежать від конкретного методу.  

Непараметричні методи не роблять конкретних припущень про закон розподілу – тільки найзагальніші (наприклад, обидві вибірки мають один закон розподілу). Вони досить строго обґрунтовані, але для багатьох багатовимірних задач  таких методів не існує. 

Надалі ми будемо розглядати критерії, в основі яких лежить припущення про нормальний закон розподілу.

Точна перевірка (критерій Пірсона) досить трудомістка, і обсяг вибірки повинен бути досить великим ( n>50), тому використовують перевірку умов, що є наслідком з нормального закону розподілу.

I  Для вибірок невеликого обсягу можна використовувати такий метод:

1)  знаходять середнє абсолютне відхилення:

Δ абс = 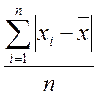              сроткл(<діапазон>);

1)  знаходять виправлене середнє квадратичне відхилення S (СТАНДОТКЛОН(<діапазон>));

2)  перевіряють умову

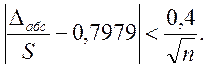                              (5.7)

Якщо ця умова виконується, то можна вважати, що гіпотеза про нормальний розподіл не суперечить наявним даним.

II  Для вибірок досить великого обсягу можна використовувати такий метод:

обчислюють   і перевіряють комплекс умов:

99,7 % відхилень від середнього менше 3σ;

2/3 (68,3%) відхилень < σ;

половина відхилень < 0,625 σ.

Якщо ці умови виконуються, то можна вважати, що гіпотеза про нормальний розподіл не суперечить наявним даним.

III  У випадку нормального розподілу оцінки асиметрії () і ексцесу (Ek) мають нормальні вибіркові розподіли, причому математичне сподівання кожного з них дорівнює нулю, а дисперсії визначаються виразами

,

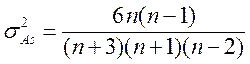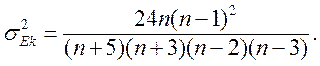
На практиці можна користуватися таким наближеним критерієм згоди

Скачать файл