Статистична перевірка гіпотез є другим після статистичного оцінювання параметрів розподілу і в той же час найважливішим розділом математичної статистики.
Методи математичної статистики дозволяють перевірити:
ü припущення про закон розподілу деяких випадкових величин (генеральної сукупності);
ü про значення параметрів цього розподілу;
ü про наявність кореляційної залежності між випадковими величинами, визначених на множині об'єктів однієї і тієї ж генеральної сукупності.
Статистичною називають гіпотезу про вигляд невідомого розподілу, про параметри відомих розподілів.
Наприклад:
1 генеральна сукупність розподілена за нормальним законом;
2 математичні сподівання двох нормальних сукупностей рівні;
3 Земля обертається навколо Сонця – нестатистична гіпотеза.
Задача полягає в тому, щоб підтвердити або спростувати гіпотезу, використовуючи вибіркові (експериментальні) дані.
Перевірити статистичну гіпотезу – це означає перевірити, чи узгоджуються вибіркові дані з цією гіпотезою. Перевірка здійснюється за допомогою статистичного критерію.
Статистичний критерій – це випадкова величина, закон розподілу якої (разом із значеннями параметрів) відомий у випадку, якщо прийнята гіпотеза справедлива.
Цей критерій ще називають критерієм згоди.
Звичайно використовуються критерії Стьюдента, Фішера, χ2 (Пірсона) та ін.
Нульовою (основною) гіпотезою називають висунуту гіпотезу Н0. Разом з нульовою гіпотезою Н0 висувається альтернативна або конкуруюча гіпотеза Н1 , що суперечить нульовій.
Наприклад :
1) Н0 : Q1 = Q2; 2) Н0 : Q1 = Q2; 3) Н0 : Q1 = Q2;
Н1 : Q1 > Q2
; Н1 : Q1 < Q2; Н1
: Q1 ![]() Q2.
Q2.
Нехай випадкова величина К – статистичний критерій перевірки деякої гіпотези Н0. При справедливості Н0 закон розподілу випадкової величини К характеризується деякою відомою щільністю розподілу ймовірності p(K).
Виберемо деяку малу величину α (0,05; 0,01; 0,001). Визначимо критичне значення критерію Ккр як розв’язок одного з трьох рівнянь залежно від вигляду Н0 та Н1 .
Р (K > Kкр)= α , (5.1)
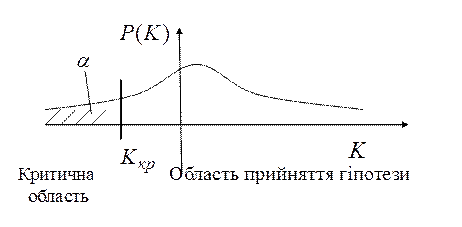
Р (K < Kкр)= α , (5.2)
Р (K < Kкр1) + Р (K > Kкр2)= α. (5.3)
Можливі й інші рівняння, але вони зустрічаються не так часто.
Розв’язок рівнянь (5.1–5.3) полягає в такому: за заданою імовірністю α, знаючи p(K), задану, як правило, у вигляді таблиць, потрібно визначити Kкр.
Розглянемо рівняння Р (K > Kкр)=
α (5.1). Розв’язавши його, знаходимо значення ![]() , що
розбиває числову вісь на дві області:
, що
розбиває числову вісь на дві області: ![]() –
область прийняття гіпотези;
–
область прийняття гіпотези; ![]() – критична область.
– критична область.
Критична точка, що отримана з рівняння (5.1), називається правобічною.
Якщо Kр
– значення критерію K, розраховане за вибірковими даними,
перевершило значення Kкр, це означає, що вибіркові дані не
дають підстави для прийняття нульової гіпотези H0. У
цьому випадку говорять, що гіпотеза H0 не узгоджується
з вибірковими даними і повинна бути відкинута. Якщо Kр не
перевершує Kкр, то говорять, що вибіркові дані не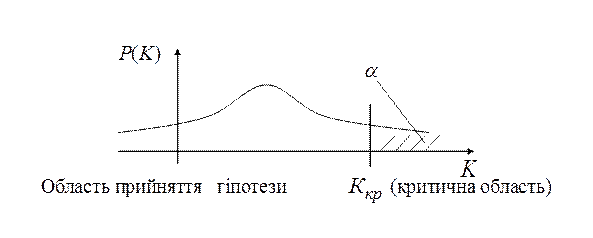 суперечать
гіпотезі H0, і немає
підстав відкидати цю гіпотезу.
суперечать
гіпотезі H0, і немає
підстав відкидати цю гіпотезу.
Правило: якщо ![]() –
– ![]() відкидається;
відкидається;
![]() –
– ![]() – приймається.
– приймається.
Рівняння (5.2) визначає лівосторонню критичну область.
Правило: ![]() –
– ![]() – відкидається ,
– відкидається ,
![]() –
– ![]() – приймається.
– приймається.
Рівняння (5.3) визначає двосторонню критичну область.
Звичайно ![]() і
і ![]() визначають таким чином, щоб виконувалася
умова
визначають таким чином, щоб виконувалася
умова
![]() .
.
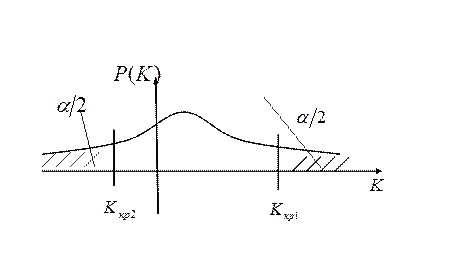
Правило:
![]() –
– ![]() – відкидається
,
– відкидається
, ![]() –
– ![]() – приймається.
– приймається.
Як бачимо, вигляд критичної області залежить від того, яка гіпотеза висунута як конкуруюча.
Помилки першого і другого роду
Ймовірність α називають рівнем значущості. Це ймовірність здійснення помилки першого роду, тобто відкидання гіпотези Н0, коли вона вірна.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.