Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 7

Варіант		Значення випадкової величини та її ймовірності
1	xi		105	110	115	120	125	130	135
	pi		0,04	0,06	0,1	0,4	0,2	0,12	0,08
2	xi		12,5	13	13,5	14	14,5	15	15,5
	pi		0,05	0,15	0,40	0,25	0,08	0,04	0,03
3	xi		10,2	10,9	11,6	12,3	13,0	13,7	14,4
	pi		0,08	0,10	0,60	0,12	0,05	0,03	0,02
4	xi		45	50	55	60	65	70	75
	pi		0,04	0,06	0,10	0,40	0,20	0,12	0,08
5	xi		110	115	120	125	130	135	140
	pi		0,05	0,10	0,30	0,25	0,15	0,10	0,05
6	xi		12,4	16,4	20,4	24,4	28,4	32,4	36,4
	pi		0,05	0,15	0,40	0,25	0,08	0,04	0,03
7	xi		26	32	38	44	50	56	62
	pi		0,05	0,15	0,40	0,25	0,08	0,04	0,03
8	xi		10,6	15,6	20,6	25,6	30,6	35,6	40,6
	pi		0,08	0,10	0,60	0,12	0,05	0,03	0,02
9	xi		100	110	120	130	140	150	160
	pi		0,04	0,06	0,10	0,40	0,20	0,12	0,08
10	xi		130	140	150	160	170	180	190
	pi		0,05	0,10	0,30	0,25	0,15	0,10	0,05

3 НОРМАЛЬНИЙ РОЗПОДІЛ І ОСНОВНІ РОЗПОДІЛИ, ПОВ'ЯЗАНІ З НИМ

3.1    Нормальний розподіл

Більшість імовірнісних методів базується на тому, що варіювання ознак підлягає визначеному закону розподілу. Ознаки об'єктів природного походження найчастіше розподілені нормально, тобто підлягають нормальному закону розподілу («закону Гаусса»). Головна особливість закону Гаусса полягає в тому, що він є граничним законом, до якого наближаються за певних умов інші закони розподілу. Нормальний закон найбільш часто зустрічається на практиці.

Для нормального закону розподілу щільність розподілу має вигляд

 ,

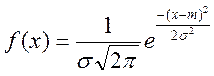де m – математичне сподівання;

 σ – середнє квадратичне відхилення ( – дисперсія).

Скорочено записують N (m, ).

Як впливає зміна параметрів m та σ на форму кривої Гаусса? Очевидно, що зміна m не змінює форму нормальної кривої (графіки функції f(x) і f(x -m ) мають однакову форму; графік f(x - m) будують шляхом зсуву графіка функції f(x) на m одиниць праворуч, якщо m > 0, і ліворуч, якщо m < 0).

Зі зміною σ максимальна ордината точки кривої змінюється. Оскільки площа, обмежена кривою розподілу, дорівнює одиниці при будь-якому значенні σ, то із зростанням σ крива Гаусса стає більш пологою, розтягується уздовж осі Ох .

На рис. 3.1 зображені нормальні криві при різних значеннях σ (σ₁ < σ < σ₂) і  деякому значенні m (однаковому для всіх трьох кривих).

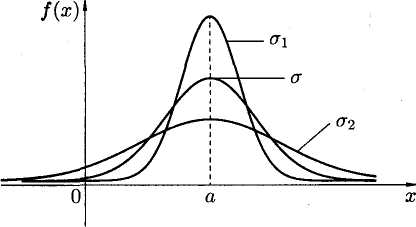
Рисунок 3.1 – Нормальні  криві при різних значеннях σ (σ₁ < σ < σ₂).

Нормальному закону підлягають помилки вимірювань, величини зношування деталей у механізмах, ріст людини, помилки пострілів, вага бульб картоплі, величина шуму в радіо-прийомному пристрої, коливання курсу акцій та ін.