Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 8

Стандартним нормальним розподілом називається розподіл з  m=0 і σ =1: ,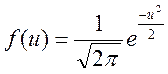

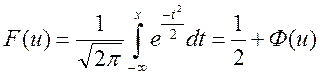 – функція розподілу,

де –функція Лапласа. Це таблична функція, її значення протабульовані. 

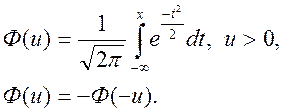
Введемо в розгляд 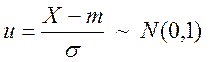 - стандартний нормальний розподіл.

.

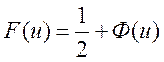Тоді ймовірність попадання випадкової величини X ~ N(m, σ) на заданий проміжок (x₁,x₂) буде дорівнювати         

.

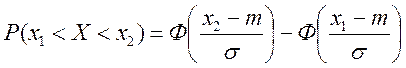3.1.1 Обчислення ймовірності заданого відхилення від математичного сподівання

Часто потрібно обчислити ймовірність того, що відхилення нормально розподіленої випадкової величини Х від математичного сподівання m за абсолютною величиною менше заданого , тобто .

,       ,

 ,

.

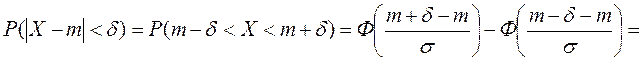
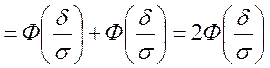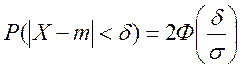Ймовірність того, що випадкова величина X набере значення, що відхиляється від математичного сподівання не більш ніж на задане (), більша в тієї величини, у якої  менше. На рис. 3.2 наведено графік для випадку, якщо m = 0,  σ₁<σ₂.

 

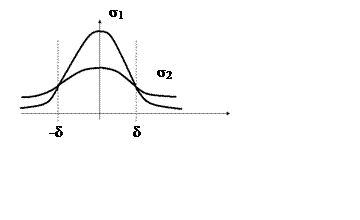Рисунок 3.2 – Графік  для випадку, якщо m = 0,  σ₁<σ₂

3.1.2 Правило трьох сигм  (3σ)

Ймовірність того, що випадкова величина X набере значення, що відхиляється від математичного сподівання не більше ніж на задане (), дорівнює

.

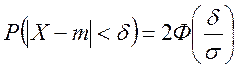Нехай , тоді

.

Якщо , тоді .

.

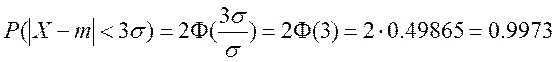Якщо випадкова величина розподілена нормально, то абсолютна величина відхилення від математичного сподівання не перевищує значення 3σ.

На практиці: якщо розподіл випадкової величини невідомий, але правило 3σвиконується, то є підстави припускати, що досліджувана випадкова величина розподілена нормально.

На нормальному законі розподілу базується практично вся параметрична статистика. Це пов'язано з тим, що більшість розподілів, що використовуються для перевірки статистичних гіпотез (Фішера, Стьюдента та ін.), є перетвореннями нормального закону  розподілу.

Головна особливість нормального закону полягає в тому, що він є граничним законом, до якого прагнуть (при виконанні деяких вимог) всі інші закони розподілу.

В Excel існує 5 функцій, пов'язаних з обчисленням нормального розподілу.

НОРМСТРАСПР(x) – повертає значення ймовірності стандартного нормального розподілу для x.

НОРМСТОБР (ймовірність) – повертає значення x для стандартного нормального розподілу для заданої ймовірності.

НОРМРАСП(x, математичне сподівання, середнє квадратичне відхилення, ознака) –  повертає значення функції щільності розподілу, якщо ознака =0, повертає значення функції розподілу, якщо ознака =1.

НОРМОБР(ймовірність, математичне сподівання, середнє квадратичне відхилення) – повертає значення x функції розподілу.

НОРМАЛИЗАЦИЯ(x, математичне сподівання, середнє квадратичне відхилення) – повертає нормоване значення  x.

3.1.3 Моменти

Початковим моментом n порядку  випадкової  величини  називають математичне сподівання величини .

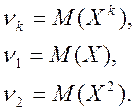
Центральним моментом порядку випадкової величини  називають математичне сподівання величини :

μ_k = М(Х - МХ)^k.

3.1.4 Оцінка відхилення теоретичного розподілу від нормального. Асиметрія та ексцес

При вивченні розподілів, відмінних від нормального, виникає необхідність кількісно оцінити цю розбіжність.

З цією метою вводять спеціальні характеристики: асиметрію та ексцес. Для нормального розподілу вони дорівнюють нулю.

Тому якщо для досліджуваного розподілу вони мають невеликі значення, то можна припустити близькість цього розподілу до нормального і навпаки.

Асиметрією теоретичного розподілу називають величину

A_s=μ₃/σ³.

Для симетричних розподілів центральні моменти непарних порядків дорівнюють 0, а отже, і A_s =0.

Якщо A_s > 0, то крива розподілу більш полога праворуч від М₀ (Х) (рис. 3.3).

Якщо A_s < 0, то крива розподілу більш полога ліворуч від М₀ (Х)  (рис. 3.4).

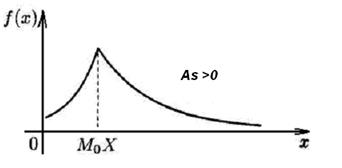
Рисунок 3.3 – Крива  розподілу для А_s > 0

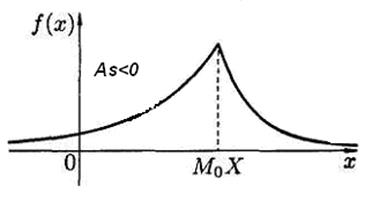
Рисунок 3.4 – Крива  розподілу для А_s < 0

Для оцінки «крутості», тобто більшого або меншого підйому теоретичного розподілу в порівнянні з нормальною кривою користуються характеристикою ексцес.

Ексцес теоретичного розподілу

.

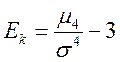Для нормального розподілу μ₄/σ⁴=3, отже,  E_k=0.