Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 3

б) шкала порядку. Можливі операції порівняння об'єктів за величиною (<, >, =, ≠). Приклад: шкала твердості мінералів, ступінь захворювання. Значення, виставлені різними експертами, можуть відрізнятися, оскільки мають суб'єктивний характер;  

в) шкала інтервалів. Можливі не тільки операції порівняння більше або менше, але і «на скільки більше (менше)» (=, ≠, <, >, +, -);

г) шкала відношення. Користуючись цією шкалою можна відповісти на  запитання «у скільки разів більше (менше)» значення величини (=, ≠, <, >, +, -, *, /).

1.4 Види шкал

Всі шкали можна умовно поділити на дискретні та неперервні.

В загальному випадку до дискретних шкал належать шкали класифікації і порядку. У цих шкалах не існує проміжних значень, їх часто називають некількісними.

До неперервних шкал відносять шкали інтервалів і відношення. 

Назва шкали	Вид шкали	Можливі операції
Класифікації	Дискретна	=, ≠
Порядку	Дискретна	=, ≠, <, >
Інтервалів	Неперервна	=, ≠, <, >, +, -
Відношення	Неперервна	=, ≠, <, >, +, -, *, /

1.5 Зв'язок шкал вимірювань і застосовуваних методів

В залежності від типу шкали вимірювання змінних для дослідження зв’язків між ними використовують різні статистичні методи (табл. 1.1).

Таблиця 1.1 – Зв’язок шкал вимірювання та методів, що застосовуються

Шкала вимірювань змінних, що впливають	Шкала вимірювань залежних змінних	Методи, що застосовують
Інтервалів або відношення	Інтервалів або відношення	Кореляційний і регресійний аналіз
Найменувань або порядку	Інтервалів або відношення	Дисперсійний аналіз
Найменувань або порядку	Найменувань або порядку	Ранговий аналіз, аналіз таблиць
Найменувань або порядку	Інтервалів або відношення	Дискримінантний аналіз, кластерний аналіз

Питання і завдання до розділу 1

1 Для чого необхідні математичні моделі.

2 Детерміновані моделі. Наведіть приклад.

3 Стохастичні моделі. Їх особливості. Наведіть приклади стохастичних моделей.

4 Предмет математичної статистики. ЇЇ роль у аналізі даних.

5 Дайте визначення вимірювання.

6 Шкали вимірювання. Дайте характеристику кожній шкалі.

7 Наведіть приклади для кожного типу шкал.

2 ВИПАДКОВІ ВЕЛИЧИНИ

Для дослідження закономірностей, що виявляють себе через випадковість, досліджують закони розподілів випадкових величин та їх числові характеристики.

Випадковою називається величина, що у результаті експерименту набуває певного числового значення, причому заздалегідь невідомо, якого саме. Дискретною випадковою величиною називається величина, що набирає окремі ізольовані значення (наприклад, кількість народжених дітей). Неперервною є величина, можливі значення якої заповнюють деякий інтервал (наприклад, маса тіла немовляти).

Незалежні випадкові величини – це величини, що є результатом незалежних випадкових подій, тобто таких подій, для яких поява однієї події ніяк не впливає на ймовірність появи іншої.

2.1 Закон розподілу

2.1.1 Закон розподілу дискретної випадкової величини

Закон розподілу – відповідність між значеннями випадкової величини і ймовірностями їх  реалізації. Закон розподілуможе бути заданий у вигляді таблиці, формули  або графіка.

Табличне подання

X	x1	x2	…	xn
P	p1	p2	…	pn

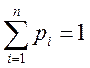,  оскільки х₁,х₂,..х_n – повна група подій

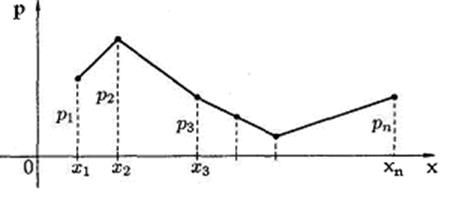
Рисунок 2.1 – Многокутник розподілу (графічне подання)

Функція розподілу – це функція F(x), що задає ймовірність того, що випадкова величина X у випробуванні набере значення менше, ніж задане х.

F(x)=P(X<x).

Іноді її називають інтегральною функцією розподілу.