Якщо Zр < Zкр.одностороннє – приймаємо гіпотезу Н0;
Zр > Zкр.одностороннє – приймаємо гіпотезу Н1.
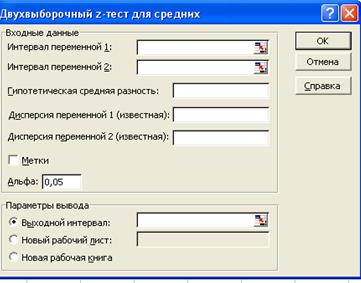
Вибираємо в пакеті Анализ данных – Двухвыборочный Z–тест для средних.
|
Двухвыборочный z-тест для средних |
||
|
Переменная 1 |
Переменная 2 |
|
|
Среднее |
||
|
Известная дисперсия |
||
|
Наблюдения |
||
|
Гипотетическая разность средних |
||
|
Z |
||
|
P(Z<=z) одностороннее |
||
|
z критическое одностороннее |
||
|
P(Z<=z) двухстороннее |
||
|
z критическое двухстороннее |
||
Z – відповідає Zр , що розраховане за даними вибірками,z критическое одностороннее – використовують для задач, що відповідають випадку (5.15) (Zкр.одностороннє); z критическое двухстороннее – використовують для задач, що відповідають випадку (5.14) (Zкр.двостороннє).
5.5.4 Перевірка гіпотези про рівність
середніх
при зв'язаних вибірках
Призначення: перевірка рівності середніх двох генеральних сукупностей, з яких витягнуті дві вибірки, за умови, що вибірки пов'язані. Наприклад, значення якихось параметрів до й після лікування, значення твердості сталі до і після загартування та ін.
Обидві вибірки витягнуті із сукупності, що має нормальний розподіл. Дані незалежні. Вибірки пов'язані.
Критеріальне значення обчислюється за формулою
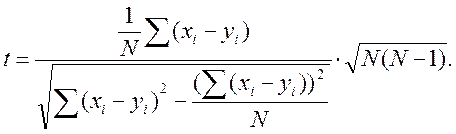
Це t – розподіл Стьюдента з k=N-1 ступенями вільності.
Правила вибору правильної гіпотези аналогічні 5.5.1 (таблиця 5.2).
Пакет Анализ данных –Парный двухвыборочный t-тест для средних.
Приклад. При дослідженні згортання крові до і після лікування вимірювали рівень фібриногену. Чи мала дана терапія вплив на активність тромбоцитів? Рівень значущості a=0,05.
|
До лікування |
1 |
1,3 |
1,4 |
0,9 |
1,2 |
1,8 |
1,1 |
1,1 |
0,7 |
0,8 |
|
Після лікування |
0,9 |
1,3 |
1,0 |
0,8 |
1,1 |
1,6 |
0,9 |
0,9 |
0,6 |
0,6 |
Висуваємо гіпотези:
Н0 : ![]()
![]() , Н1 :
, Н1 : ![]() .
.
|
Парный двухвыборочный t-тест для средних |
||
|
Переменная 1 |
Переменная 2 |
|
|
Среднее |
1,13 |
0,97 |
|
Дисперсия |
0,102333333 |
0,093444444 |
|
Наблюдения |
10 |
10 |
|
Корреляция Пирсона |
0,941947543 |
|
|
Гипотетическая разность средних |
0 |
|
|
df |
9 |
|
|
t-статистика |
4,706787243 |
|
|
P(T<=t) одностороннее |
0,000554759 |
|
|
t критическое одностороннее |
2,262158887 |
|
|
P(T<=t) двостороннее |
0,001109517 |
|
|
t критическое двостороннее |
2,685010259 |
|
Як видно з таблиці, tр=4,707, t кр= 2,685. Оскільки tр > tкр, приймаємо гіпотезу Н1.
Висновок: Дана терапія впливає на активність тромбоцитів.
5.5.5 Порівняння вибіркової середньої (з генеральної нормальної сукупності) із заданим а
Будуємо випадкову величину, що має розподіл Стьюдента
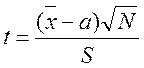 ,
,
з N-1 ступенями вільності, де N – розмір вибірки, S – середнє квадратичне відхилення.
1 Випадок перевірки гіпотез
Н0: ![]() , H1:
, H1: ![]() .
.
Якщо |![]() р
|<t кр.двостороннє приймаємо H0
р
|<t кр.двостороннє приймаємо H0 ![]() ,
,
|![]() р
|> t кр.двостороннє приймаємо H1
р
|> t кр.двостороннє приймаємо H1 ![]() .
.
2 Перевіряємо гіпотези
Н0: ![]() , H1:
, H1: ![]() .
.
При заданому рівні значущості α знаходимо tкр.правостороннєз рівняння
![]() .
.
![]() – однобічна
(правостороння) критична точка.
– однобічна
(правостороння) критична точка.
Якщо ![]() р
<
р
<![]() , приймаємо H0 :
, приймаємо H0 : ![]() .
.
Якщо ![]() р
>
р
>![]() , приймаємо H1:
, приймаємо H1: ![]() .
.
3 Перевіряємо гіпотези
Н0: ![]() , H1:
, H1: ![]() .
.
При заданому рівні значущості α знаходимо tкр.лівосторннє з рівняння
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.