Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 24

Умови:

   – вибірки розподілені нормально;

   – дисперсії невідомі і різні;

   – дані незалежні.

Використовується критерій Стьюдента

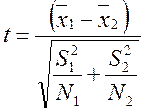,                          (5.12)

де K – число ступенів вільності, обчислюється таким чином:

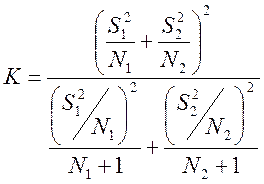–2,

де N₁, N ₂  – розміри вибірок; виправлені дисперсії;

оцінки середніх значень.

Правила вибору правильної гіпотези аналогічні 5.5.1 (таблиця 5.2).

В Excel Сервис – Анализ данных – Двухвыборочный
t-тест с разными дисперсиями.

Приклад. На заводі з метою контролю вмісту марганцю в одній з марок сталі зробили 10 відливів з конвертора 1 і стільки ж з конвертора 2.  Чи можна вважати вміст марганцю в сталі, виплавленій в цих конверторах, однаковим з рівнем значущості a=0,05?

Конвертор 1	Конвертор 2
1,05	1,38
1,11	1,34
1,14	1,32
1,17	1,30
1,18	1,38
1,21	1,35
1,25	1,35
1,14	1,32

Задача зводиться до перевірки гіпотези про рівність середніх значень двох вибірок. Але спочатку необхідно перевірити, чи значущо відрізняються їх дисперсії.

Для перевірки рівності дисперсій  висуваємо такі гіпотези:

H₀: S₁=S₂;    H₁: S₁≠S_2.

F_кр  знаходимо з рівняння ; α/2=0,025.

Обираємо Сервис – Анализ данных – Двухвыборочный F-тест для дисперсии. Отримаємо такі дані.

Двухвыборочный F-тест для дисперсии
	Переменная 1	Переменная 2
Среднее	1,15625	1,3425
Дисперсия	0,003769643	0,000821429
Наблюдения	8	8
df	7	7
F	4,589130435
P(F<=f) одностороннее	0,031104627
F критическое одностороннее	4,994888059

Як бачимо з таблиці  F_p= 4,589, F_кр=3,787. Оскільки F_p>F_кр , гіпотезу H₀ відхиляємо. Отже, дисперсії не рівні, тобто S₁≠S₂.

Перевіряємо, чи можна вважати рівними середні значення вибірок. Висуваємо гіпотези

,  .

Вибираємо в пакеті Анализ данных – Двухвыборочный t-тест с разными дисперсиями.

Двухвыборочный t-тест с разными дисперсиями
	Переменняа 1	Переменная 2
Среднее	1,15625	1,3425
Дисперсия	0,003769643	0,000821429
Наблюдения	8	8
Гипотетичческая разность средних	0
df	10
t-статистика	-7,774710921
P(T<=t) одностороннее	7,55449E-06
t критическое одностороннее	2,228139238
P(T<=t) двостороннее	1,5109E-05
t критическое двостороннее	2,633769327

Як бачимо з таблиці t_p=-7,775, t_{кp.двост}=2,634. Оскільки |t_р|>t_кр,  приймаємо гіпотезу Н₁.

Висновок: не можна вважати вміст марганцю в сталі однаковим у цих конверторах.

5.5.3 Перевірка гіпотез про середні з довільно  розподіленими дисперсіями (вибірки великі n >30, незалежні)

Якщо вибірки великого обсягу, то вибіркові дисперсії є досить гарними оцінками генеральних дисперсій, а вибіркові середні розподіляються приблизно нормально. Критерій

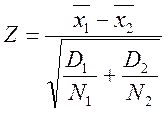,                                          (5.13)

де D₁ та   D₂ – дисперсії вибірок; розміри вибірок;

 – середні значення вибірок.

Z розподілено за стандартним нормальним законом N (0; 1).

1. Висуваємо гіпотези:

Н₀ :  ,           Н₁ :    .

Тоді Z_{кр.двостороннє} обчислюємо за допомогою функції Лапласа

Ф (Z_кр) = (1-α)/2.                   (5.14)

Якщо Z_р < Z_{кр двостороннє} – приймаємо гіпотезу Н₀,

            Z_р > Z_{кр двостороннє} – приймаємо гіпотезу Н₁.

2. Висуваємо гіпотези:

Н₀ :  ,           Н₁ :    ^.

Тоді Z_{кр.одностороннє} обчислюємо за допомогою функції Лапласа

Ф (Z_{кр.одностороннє}) = (1-2 α)/2.                       (5.15)