Информатика и выч. техника \ Анализ данных

Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 18

Чим менший рівень значущості, тим менша ймовірність відкинути гіпотезу H0, що перевіряється, коли вона правильна, тобто зробити помилку першого роду. Але зі зменшенням рівня значущості розширюється область прийняття гіпотези H0 і збільшується ймовірність прийняття гіпотези, що перевіряється, коли вона неправильна, тобто коли перевага повинна бути віддана конкуруючій гіпотезі. Ця помилка називається помилкою другого роду, b  – ймовірність помилки другого роду.

Число 1 – b, рівне імовірності того, що не відбувається помилка другого роду, називається потужністю критерію.

Вибір статистичного критерію і вигляду критичної області здійснюється таким чином, щоб потужність критерію була максимальною.

5.1 Перевірка гіпотези про закон розподілу

У багатьох випадках закон розподілу досліджуваної випадкової величини невідомий, але є підстави припустити, що він має цілком певний вигляд: нормальний, біноміальний або який-небудь інший.

Нехай необхідно перевірити гіпотезу Н0 про те, що вибірка підкоряється певному закону розподілу, заданому функцією F0(x). Під альтернативною гіпотезою H1 в цьому випадку будемо підрозумівати те, що просто не виконано основну гіпотезу.

Потрібно зробити висновок:  чи погоджуються результати спостережень із висловленим припущенням. Для цього використаємо спеціально підібрану величину – критерій згоди.

Критерієм згоди називають статистичний критерій перевірки гіпотези про передбачуваний закон невідомого розподілу. Він використовується для перевірки згоди передбачуваного виду розподілу з досліджуваними даними на підставі вибірки.

Існують різні критерії згоди: Пірсона, Колмогорова, Фішера, Смирнова та ін.

Критерій згоди Пірсона – найбільш часто вживаний критерій для перевірки гіпотези про закон розподілу.   

Для перевірки гіпотези про закон розподілу необхідно розрахувати емпіричні і теоретичні частоти.

5.1.1 Емпіричні та теоретичні частоти. Безперервний розподіл

Нехай при дослідженні випадкової величини була отримана вибірка розміром n. Весь інтервал можливих значень поділяють на k інтервалів. Інтервали не перетинаються і рівні між собою. Потім обчислюють  – кількість значень, що потрапили в i-й інтервал. Емпіричними називають частоти ni, що фактично спостерігаються .

Теоретичні частоти безперервного розподілу знаходять за формулою

,                                  (5.4)

де N – число випробувань;

– ймовірність влучення X у i-й частковий інтервал, обчислена при допущенні, що X має функцію розподілу F(x).

                      (5.5)

Зокрема, якщо є підстави припускати, що випадкова величина X розподілена нормально, то теоретичні частоти, обчислюють таким чином

де  N – число випробувань;

– права границя i-го інтервалу;

 – середнє значення; 

 S – стандартне відхилення.

5.1.2 Критерій згоди Пірсона

Нульова гіпотеза: генеральна сукупність розподілена за законом F(x). В якості критерію обираємо випадкову величину 

c2 р= 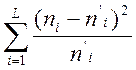,                           (5.6)

де ni – емпіричні частоти;

ni’  – теоретичні частоти.

Для рівня значущості α знаходимо c , розв’язуючи рівняння

P(c > c )= α,

c2кр=Хи2Обр(α,K),

де   K = L - 1 - r ;

L – число часткових інтервалів;

r – число параметрів розподілу. Для нормального закону r = 2.

Якщо c2 р  <  c  – гіпотезу про закон розподілу приймаємо.

Якщо   c2 р  >  c– гіпотезу Н0 відкидаємо.

Обсяг вибірки повинен бути більше  ніж 50.

Приклад. У таблиці наведені значення частот.  Розрахувати теоретичні частоти в припущенні, що вибірка підпорядковується нормальному закону розподілу. Відомо, що  =42,37,  S=0,94.З рівнем значущості 0,01 перевірити гіпотезу про закон розподілу.

i

0

1

2

3

4

5

інтервали

(-∞;40]

(40;41]

(41;42]

(42;43]

(43;44]

(44;46]

ni – емпіричні частоти

0

20

112

154

73

15
Скачать файл