М(CX) = CM(X).
3 Математичне сподівання суми випадкових величин дорівнює сумі їх математичних сподівань
М(Х + Y) = M(X) + M(Y).
4 Математичне сподівання відхилення випадкової величини від її математичного сподівання дорівнює нулю:
М(Х – M(X)) = 0.
5 Математичне сподівання добутку незалежних випадкових величин дорівнює добутку їх математичних сподівань:
М(Х · Y) = M(X) · M(Y).
2.2.2 Дисперсія випадкової величини
Дисперсія випадкової величини визначається як математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання:
![]() ,
,
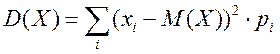 - для
дискретної випадкової величини Х,
- для
дискретної випадкової величини Х,
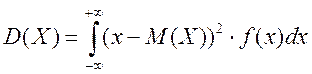 - для неперервної
випадкової величини Х.
- для неперервної
випадкової величини Х.
Дисперсія звичайно розраховується за формулою
![]() .
.
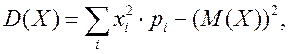 для дискретної
випадкової величини Х,
для дискретної
випадкової величини Х,
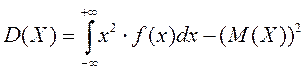 ,
для неперервної випадкової величини Х.
,
для неперервної випадкової величини Х.
Дисперсія дозволяє оцінити розсіювання можливих значень випадкової величини відносно її середнього значення.
Властивості:
1 Дисперсія постійної дорівнює нулю
D(С) = 0.
2 Постійний множник можна виносити за знак дисперсії, звівши його у квадрат
D(СХ) = С2D(X).
3 Дисперсія суми незалежних випадкових величин дорівнює сумі їх дисперсій
D(X+Y)=D(X)+D(Y).
4 Дисперсія випадкових величин не зміниться, якщо до цієї випадкової величини додати постійну
D(X + С)= D(X).
5 Якщо випадкові величини X і Y незалежні:
D(XY) = MX2 · MY2 - (МХ)2·(МY)2.
2.2.3 Середнє квадратичне відхилення випадкових величин
Дисперсія D(X) має розмірність квадрата випадкової величини X, що є незручним при порівнянні. Коли бажано, щоб оцінка розкиду (розсіювання) мала розмірність випадкової величини, використовують ще одну числову характеристику – середнє квадратичне відхилення.
Середнім квадратичним відхиленням або стандартним відхиленням випадкової величини X називається квадратний корінь із її дисперсії, позначають його через σ(Х) (або σХ). Таким чином, за визначенням
![]() .
.
2.2.4 Мода і медіана
Модою дискретної випадкової величини X називається її значення, набуте з найбільшою ймовірністю в порівнянні з двома сусідніми значеннями, позначається через М0 (Х). Для неперервної випадкової величини M0 (X) - точка максимуму (локального) щільності f(x).
Якщо мода єдина, то розподіл випадкової величини називається унімодальним, у протилежному разі – полімодальним.
Медіаною Ме (Х) неперервної випадкової величини X називається таке її значення хр, для якого
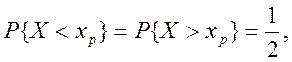
тобто однаково ймовірно, що випадкова величина X виявиться менше хр або більше хр .
Для дискретної випадкової величини X медіана звичайно не визначається.
 x
x
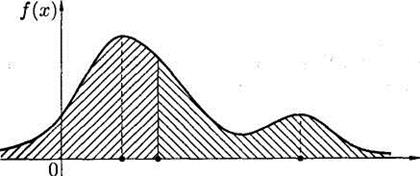
М0 (Х) хр=Ме (Х) М0 (Х)
Рисунок 2.6 – Мода та медіана для неперервної випадкової величини
Приклад. Дано закон розподілу дискретної випадкової величини Х.
|
Х |
2 |
4 |
8 |
10 |
|
Р |
0,4 |
0,2 |
0,1 |
0,3 |
Побудувати многокутник розподілу, визначити функцію розподілу, математичне сподівання, дисперсію, середнє квадратичне відхилення. Побудувати графік функції розподілу.
Многокутник розподілу
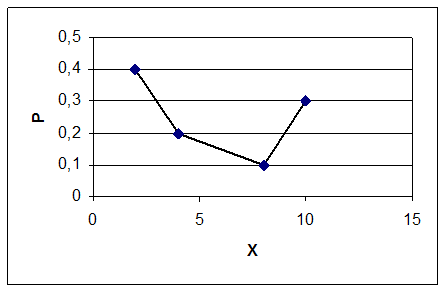
Функція розподілу:
|
Х |
2 |
4 |
8 |
10 |
|
Р |
0,4 |
0,2 |
0,1 |
0,3 |
|
F(x) |
0,4 |
0,6 |
0,7 |
1 |
Аналітичний вигляд функції розподілу:
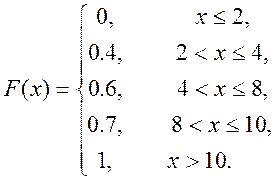
Графік функції розподілу
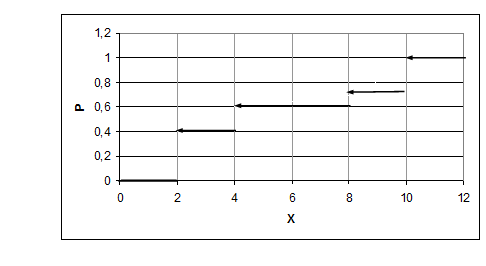
Математичне сподівання, дисперсія, середнє квадратичне відхилення обчислюються в такий спосіб:
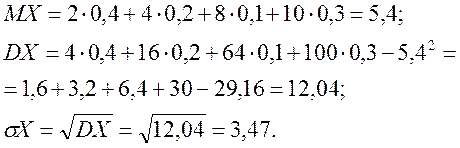
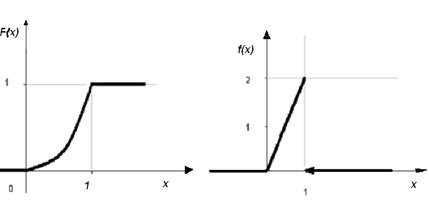
Приклад. Задана функція розподілу неперервної випадкової величини X:
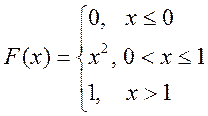
Визначити: M(X) - математичне сподівання, D(X) – дисперсію, ймовірність улучення значення випадкової величини в інтервал Р(0,5<X<1). Побудувати графіки функцій розподілу та щільності розподілу.
Функція щільності розподілу.
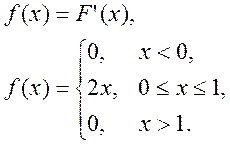
Перевіряємо свої обчислення
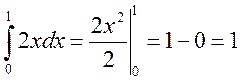 .
.
Обчислюємо M(X) - математичне сподівання
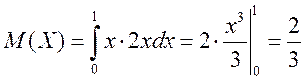 .
.
Обчислюємо D(X) – дисперсію
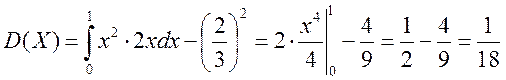 .
.
Обчислюємо ймовірність потрапляння значення випадкової величини в інтервал Р(0,5<X<1)
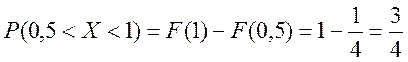 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.