З’ясувати, чи можна вважати точність вимірювання кожним мікроскопом однаковою?
21 Номінальний опір резистора 2000 Ом. Для контролю відібрано партію з 12 резисторів. Після вимірювання опору кожного точністю до 5 Ом одержано такі значення: 2130, 2090, 2030, 2080, 1920, 2020, 2015, 2000, 2945, 1940, 1980, 1970. Чи можна відхилення від номіналу (2000 Ом) розглядати як випадкові (допустимі), чи, навпаки, результати вимірювань свідчать про те, що опір резисторів істотно відрізняється від номіналу? Розв’язати поставлену задачу, сформулювавши її як задачу перевірки статистичних гіпотез?
У багатьох завданнях потрібно встановити й оцінити залежність досліджуваної випадкової величини від однієї або декількох інших величин.
Випадкові величини можуть бути пов’язані або функціональною залежністю, або статистичною, або бути незалежними.
Функціональний зв'язок - кожному значенню змінної X поставлене в однозначну відповідність певне значення Y.
Статистичний зв'язок – зміна однієї з величин приводить до зміни закону розподілу іншої.
Якщо статистична залежність проявляється в тому, що при зміні однієї з випадкових величин змінюється середнє значення іншої, то таку залежність називають кореляційною.
6.1 Кореляційний аналіз (КА)
Кореляційний аналіз застосовується, коли змінні вимірюються в шкалах відносин, інтервалів або порядку, тобто мають числову природу.
Характеристикою залежності між випадковими величинами X і Y служить коефіцієнт коваріації.
![]() .
.
Оцінкою коефіцієнта коваріації є вибірковий коефіцієнт коваріації:
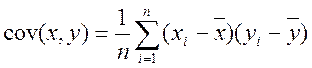 , (6.1)
, (6.1)
![]() .
.
Якщо при більших значеннях X більше
ймовірні більші значення Y, а при малих значеннях X більше
ймовірні малі значення Y, то в (6.1) додатні доданки домінують і ![]() . У цьому випадку говорять про прямий
зв'язок: із зростанням Х випадкова величина Y має
тенденцію до зростання.
. У цьому випадку говорять про прямий
зв'язок: із зростанням Х випадкова величина Y має
тенденцію до зростання.
Якщо ж більш ймовірні доданки ![]() із співмножників різних знаків, то
із співмножників різних знаків, то![]() , тобто буде мати місце зворотний
зв'язок, із зростанням X випадкова величина Y зменшується.
, тобто буде мати місце зворотний
зв'язок, із зростанням X випадкова величина Y зменшується.
Якщо ![]() , то
додатні і від’ємні доданки «гасять» один одного, і зв'язок між X і Y
не спостерігається.
, то
додатні і від’ємні доданки «гасять» один одного, і зв'язок між X і Y
не спостерігається.
Якщо X і Y незалежні,
то ![]() .
.
Зворотного висновку зробити не можна!
Випадкові величини можуть бути пов'язані функціональною залежністю, але
коефіцієнт ![]() .
.
Величина cov(x,y) – залежить від одиниць вимірювання, тому її незручно використовувати за показник зв'язку. У зв'язку з цим вводять коефіцієнт парної кореляції. Коефіцієнт парної кореляції використовують для вимірювання сили лінійних зв'язків різних пар ознак з їх множини. Вибірковий коефіцієнт парної кореляції обчислюється за формулою
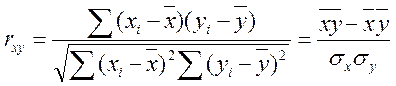
![]() , (6.2)
, (6.2)
де
xi, yi – спостережувані значення;
![]() – відповідні вибіркові середні значення для
X та Y;
– відповідні вибіркові середні значення для
X та Y;
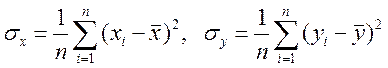 – вибіркові середні квадратичні відхилення
для X та Y;
– вибіркові середні квадратичні відхилення
для X та Y;
![]() –
обсяг вибірки.
–
обсяг вибірки.
![]() – вибіркові середні квадратичні відхилення
(не виправлені!! Функція в EXCEL СТАНДОТКЛОНП(<діапазон>)).
– вибіркові середні квадратичні відхилення
(не виправлені!! Функція в EXCEL СТАНДОТКЛОНП(<діапазон>)).
Функції в EXCEL:
КОВАР(масив1; масив2) – повертає коваріацію, тобто середнє добутків відхилень для кожної пари точок даних.
КОРРЕЛ(масив1;масив2) – повертає парний коефіцієнт кореляції. Можна також скористатися Сервис – Анализ данных – Корреляция.
6.1.1 Властивості коефіцієнта кореляції
1
Коефіцієнт кореляції приймає значення з відрізку [-1;1] ![]() .
.
2 Якщо ![]() , випадкові величини X і Y
пов'язані лінійною залежністю і цей зв'язок є функціональним.
, випадкові величини X і Y
пов'язані лінійною залежністю і цей зв'язок є функціональним.
3 Якщо rxy >0, то між змінними існує прямий лінійний зв’язок, значення змінних збільшуються або зменшуються одночасно.
Якщо rxy <0, то між змінними зворотній лінійний зв'язок, і при збільшенні однієї змінної інша зменшується.
Якщо коефіцієнт вибіркової кореляції за модулем наближається до 1, це означає, що між випадковими величинами X і Y існує лінійний статистичний зв'язок.
4 rxy =ryx.
Зауваження
1 Варто пам'ятати, що коефіцієнт кореляції показує тісноту тільки лінійного зв'язку, для більш складних залежностей (квадратичних, кубічних та ін.) коефіцієнт кореляції може показувати відсутність зв'язку. Для досліджень більш складних залежностей використовують регресійний аналіз.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.