Після того як визначений вигляд закону розподілу, необхідно оцінити його параметри. Наприклад, для нормального закону розподілу треба визначити математичне сподівання і середнє квадратичне відхилення, тому що ці параметри цілком визначають його.
Звичайно в розпорядженні дослідника є значення деякої ознаки x1…xn, отримані в результаті n незалежних спостережень.
Розглядаючи x1,x2…xn як незалежні випадкові величини X1,X2,…,Xn, можна сказати, що знайти статистичну оцінку невідомого параметра теоретичного розподілу – це означає знайти функцію від випадкових величин, що спостерігаються, яка дає наближене значення оцінюваного параметра.
Наприклад, для оцінки математичного сподівання нормального закону розподілу служить функція
.
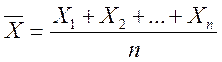Властивості оцінок параметрів
Незсуненість – це означає, що при проведенні великої кількості випробувань з вибірками будь якого розміру середнє значення кожної вибірки тяжіє до дійсного значення генеральної сукупності. Наприклад, M(Q*)= Q (математичне сподівання прирівнюється до оцінюваного параметра Q при будь-якому обсязі вибірки). Зсуненість, як правило, обумовлена наявністю систематичної помилки.
Спроможність. Із збільшенням розміру вибірки оцінка повинна наближатися до значення відповідного параметра генеральної сукупності з імовірністю, що наближається до 1.
Ефективність. Обрана оцінка для вибірок рівного обсягу повинна мати мінімальну дисперсію.
Достатність. Оцінка повинна містити всю необхідну інформацію і не вимагати додаткової.
До характеристик одновимірного розподілу відносять:
1 Міри положення (середнє, медіана, мода та інші).
2 Міри розсіювання (дисперсія, середнє квадратичне відхилення, коефіцієнт варіації, розмах).
3 Міри форми (асиметрія, ексцес, моменти 3-го і 4-го порядку).
Вибірковим середнім називається середнє арифметичне всіх значень вибірки
.
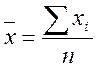Властивості
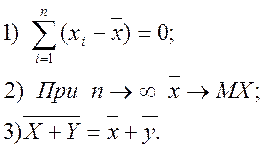
Для нормального закону розподілу 
є незсуненою оцінкою
математичного сподівання з найменшою дисперсією. В Excel для обчислення
середнього значення існує статистична функція СРЗНАЧ(< діапазон >).
Середнє геометричне обчислюється за формулою
.
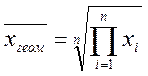Відповідна функція в Excel СРГЕОМ (< діапазон >).
Середнє гармонійне обчислюється за формулою
.
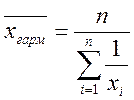Відповідна функція в Excel СРГАРМ (< діапазон >).
Мода – значення, що спостерігається найбільшу кількість разів. Позначається Мо.
Медіана – поділяє варіаційний ряд на 2 частини, рівні по числу варіантів. Позначається Ме.
Якщо n=2k+1Þ Мe=Xk+1,
n=2k Þ Мe=(Xk+Xk+1)/2.
Середнє абсолютне відхилення обчислюється за формулою
.
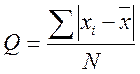Варіаційним розмахомназивається різниця між найбільшим і найменшим значеннями вибірки:
Rв=Xmax-Xmin.
Незсунена оцінка дисперсії для нормального розподілу (емпірична дисперсія).
.
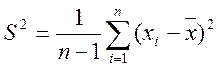Стандартне відхилення
.
Коефіцієнт варіаціїобчислюється за формулою
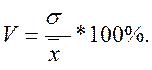
Якщо V >100% - це означає, що дані неоднорідні.
Рівняння для асиметрії визначається в такий спосіб:
.
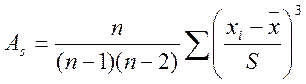Нагадаємо, що асиметрія характеризує ступінь несиметричності розподілу щодо його середнього.
Для обчислення асиметрії в Excel використовують функцію СКОС(<діапазон>).
Для оцінки «крутості», тобто більшого або меншого підйому теоретичного розподілу в порівнянні з нормальною кривою використовують ексцес, який характеризує відносну гостроту або згладженість розподілу в порівнянні з нормальним розподілом. Обчислюється за формулою
.
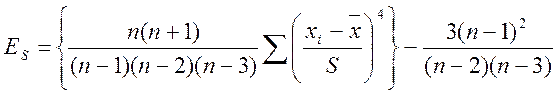Для обчислення ексцесу в Excel використовують функцію Эксцесс(<діапазон>).
Більшість з описаних параметрів і характеристик (за винятком згрупованих даних) можуть бути обчислені з використанням електронної таблиці Excel. У таблиці 4.1 наведені функції, що мають відношення до законів розподілу.
Таблиця 4.1– Функції Excel для визначення параметрів вибірки
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.