Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 15

38,839<a<45,799.

Як бачимо, при збільшенні кількості випробувань довірчий інтервал звужується.

4.6.2 Довірчий інтервал для середнього квадратичного відхилення (нормальний розподіл)

Можна показати, що якщо MX=а невідоме, то довірчий інтервал для середнього квадратичного відхилення має вигляд:

,

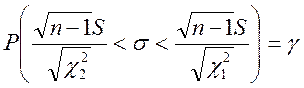де – критичне значення c² розподілу з (n-1) ступенями вільності з рівнем значущості α₁=;

– критичне значення c² розподілу з (n-1) ступенями вільності з рівнем значущості α₂=.

Таблиця для випадкової величини c² звичайно задається розв’язком рівняння .

За таблицею для заданої величини q і за числом ступенів вільності n-1 визначаємо   (функція EXCEL    ХИ2ОБР(q;  n-1)).

Приклад. За даними 20 вимірювань знайдене «виправлене» середньоквадратичне відхилення S=0,12. Знайти точність вимірів з надійністю 0,98. Точність вимірів характеризується середнім квадратичним відхиленням σ випадкових помилок. Тому задача зводиться до знаходження довірчого інтервалу, що покриває σ із заданою надійністю (0,98).

Використовуючи функцію ХИ2ОБР(q, n-1),  знайдемо  і . Для ступенів вільності  n - 1=19 і ймовірності α₂=(1-0,98)/2=0,01 знаходимо =36,2, а потім для n - 1=19 і ймовірності  α₁=(1+0,98)/2=0,99 знаходимо =7,63.

=ХИ20БР(0,01; 19)=36,2 ;

=ХИ20БР(0,99;19)=7,63.

Знаходимо

 

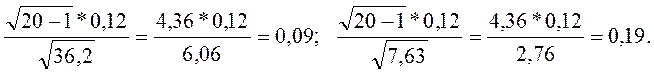
  Шуканий довірчий інтервал (0,09;0,19).

Питання і завдання до розділу 4

1 Теорема Чебишева.

2 Практичне значення теореми Чебишева.

3 Коли застосовується вибірковий метод, його суть.

4 Точкові оцінки параметрів розподілу. Їх властивості.

5 Міри положення. Формули для обчислень. Функції Excel.

6 Міри розсіювання. Формули для обчислень. Функції Excel.

7 Дайте визначення інтервальних оцінок параметрів розподілу. Довірчий інтервал. Точність. Надійність.

8 Довірчий інтервал для математичного сподівання нормального розподілу.

9 Довірчий інтервал для дисперсії (нормальний розподіл).

10 Знайдіть середнє вибірки, дисперсію й середнє квадратичне відхилення, моду, медіану за даними табл. 4.2.

Таблиця 4.2

xi	6	7	8	9	10	11	12	13	14	15
ni	5	18	32	10	17	10	3	2	2	1

11 Для визначення середнього проценту виконання норми виробітку працівникам заводу було обстежено 64 особи. Результати подані в табл. 4.3. Знайдіть середнє вибірки, дисперсію, середнє квадратичне відхилення.

Таблиця 4.3

Виконання норм виробітку, %	Чисельність робітників, осіб
До 100	2
100 – 110	11
110 – 120	24
120 – 130	14
130 – 140	8
140 і більше	5
Разом	64

13 За дев'ятьма рівноточними вимірами діаметра деталі одним приладом установлений середній діаметр см , а за шістьма рівноточними вимірами іншим приладом отриманий результат  см. Визначте найбільш точну оцінку діаметра деталі за вимірами двох приладів.

14  Як оцінити за вибіркою моду та медіану?

Лабораторна робота

Тема. Обчислення основних статистичних характеристик вибірки

У таблиці 4.4 наведена вибірка.

1  Для даних цієї вибірки побудувати гістограму.

2  Обчислити з використанням функцій Excel :

ü  середнє значення;

ü  виправлену дисперсію;

ü  виправлене середнє квадратичне відхилення;

ü  моду;

ü  медіану;

ü  асиметрію;

ü  ексцес;

ü  довірчий інтервал для математичного сподівання та середньоквадратичного відхилення з надійністю 0,95.

Таблиця 4.4