Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 21

			alfa=0,05
Двухвыборочный F-тест для дисперсий
		Переменная 1	Переменная 2
Среднее		40,57142857	42,83333333
Дисперсия		4,619047619	0,566666667
Наблюдения		7	6
df		6	5
F		8,151260504
P(F<=f) одностороннее		0,017997241
F критическое одностороннее		4,950294397

Як видно з таблиці, Excel дозволяє отримати всю необхідну інформацію для розв’язання поставленої задачі. Пояснимо, що df  – кількість ступенів вільності, F – розраховане значення F_р, F критическое одностороннее – відповідно F_кр.

F_р  >  F_кр, отже, приймаємо гіпотезу Н₁: S > S , тобто дисперсії різняться суттєво.

Висновок: можна вважати удосконалення верстата ефективним.

5.4 Порівняння виправленої вибіркової дисперсії з гіпотетичною генеральною дисперсією

На практиці ця гіпотеза перевіряється, якщо потрібно перевірити, чи відповідає точність приладів, інструментів, методів та ін. необхідному стандартові.

Наприклад: відоме припустиме розсіювання розміру s₀, а верстат забезпечує S (обчислено за вибіркою). Якщо S  значно відрізняється від s₀, то верстат вимагає налагодження.

Критерій перевірки

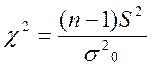,                                 (5.10)

розподіл Пірсона з  k = n – 1 ступенями вільності.

H₀: S² = s₀²,

Н₁: S² > s₀².

c_кр² обчислюємо, як розв’язок  рівняння

Р(c² > c_кр²(α,k)) = α.

Якщо  c_р < c_кр – H₀  приймається.

Приклад. Партія виробів приймається, якщо дисперсія контрольованого розміру суттєво не перевищує 0,12. Виправлена вибіркова дисперсія, знайдена за вибіркою розміром N=13 дорівнює 0,146. Чи можна прийняти партію при рівні значущості ?

H₀: S² = s₀², Н₁: S² > s₀².

Критерій перевірки

                        ,

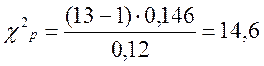χ²_кр= ХИ2ОБР(0,01; 12)=26,2.

Оскільки χ²_р  < χ²_кр приймаємо гіпотезу Н₀, тобто розбіжності між виправленою дисперсією 0,146 і генеральною дисперсією 0,12 можна  вважати несуттєвими. Висновок: партію можна прийняти.

5.5 Перевірка гіпотез про середні для нормальної генеральної сукупності

Можливі такі постановки задач:

1    Порівняння показників контрольної і експериментальної вибірок. У нас є 2 незалежні вибірки; середні значення деяких параметрів ми хочемо порівняти. Наприклад: 2 групи хворих, лікування яких проводилося різними методами. Можливі такі випадки:

·  вибірки невеликого обсягу (n<30):

- дисперсії вибірок рівні;

- дисперсії вибірок не рівні;

·  без припущення про дисперсії (вибірки великі n>30);

2     Порівняння показників вибірки до і після експерименту. У цьому випадку ми маємо справу з так званими зв'язними вибірками. Наприклад, показники твердості  матеріалу до і після відповідної обробки (загартування). «Вибірки, що відповідним чином розбиваються на пари».

3     Чи можна вважати, що деяке значення показника дорівнює деякому нормальному значенню. Наприклад, у медицині: артеріальний тиск, пульс, гемоглобін та ін.

5.5.1 Перевірка гіпотези про рівність середніх при рівних дисперсіях (малі вибірки n<30)

Умови:

1  Вибірки розподілені нормально.

2  Дисперсії невідомі й однакові: .

3  Дані незалежні.

Використовується критерій Стьюдента :

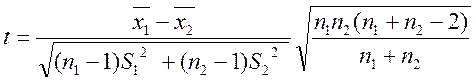      (5.11)

з k=n1+n2-2 ступенями вільності,

де обсяг вибірок;

середні значення;

виправлені дисперсії.

Залежно від вигляду конкуруючої гіпотези можливі такі випадки.

1. Для, того щоб при заданому рівні значущості α перевірити нульову гіпотезу Н₀:  про рівність середніх двох нормальних сукупностей з невідомими, але однаковими дисперсіями (у випадку незалежних малих вибірок) при конкуруючій гіпотезі Н₁: , треба обчислити розрахункове значення критерію:

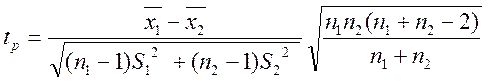
і за таблицею критичних точок розподілу Стьюдента, за заданим рівнем  значущості α (розміщеним у верхньому рядку таблиці) і числом ступенів вільності k=n1+n2 знайти критичну точку t_{двост. кр} (α; k), як розв’язок рівняння .