Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 14

Назва параметра	Назва функції	Опис параметрів
Середнє	СРЗНАЧ	Перелік значень або інтервал імен комірок
Медіана	МЕДИАНА	–„–
Мода	МОДА	–„–
Дисперсія	ДИСП	–„–
Середнє квадратичне відхилення	СТАНДОТКЛОН	–„–
Середнє геометричне	СРГЕОМ	–„–
Середнє гармонійне	СРГАРМ	–„–
Ексцес	ЭКСЦЕСC	–„–
Асиметрія	СКОС	–„–
Середнє значення абсолютних відхилень від середнього значення	СРОТКЛ	–„–
Стандартне відхилення за генеральною сукупністю	СТАНДОТКЛОНП	–„–

Розглянемо приклад використання  основних функцій.

Приклад. Обчислити основні числові характеристики для вибірки

Ν	1	2	3	4	5	6
Значення	76,7	70,1	91,2	70,7	71,5	78,6

Нижче наведена копія екрана з прикладом.

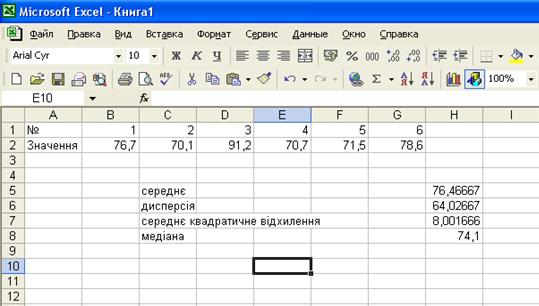
В комірках  B2 – G2 знаходяться вхідні дані. В комірках Н5 – Н8 знаходяться функції, що обчислюють необхідні нам параметри.

4.6 Довірчий  інтервал

Точковою називають оцінку, що визначається одним числом. Всі оцінки, розглянуті вище, – точкові.

Інтервальною називають оцінку, що визначається двома числами – кінцями інтервалу.

Нехай знайдена за даними вибірки точкова характеристика Q^* , яка служить оцінкою невідомого параметра Q. Будемо вважати Q=const. Q^* тим точніше визначає Q, чим менше абсолютна величина | Q - Q^* | , тобто якщо δ>0  і | Q - Q^* | <δ , то чим менше δ, тим оцінка точніша. δ – характеризує точність оцінки.

Надійністю (довірчою імовірністю) оцінки Q по Q^*  називають ймовірність γ, з якою оцінюють нерівність |Q–Q^* |<δ.

P( | Q- Q^* | <δ ) = γ.

Найчастіше задають γ = 0,95;  0,99 і 0,999.

Перейшовши до подвійної нерівності, отримаємо

P(Q^*  - δ < Q < Q^* + δ ) = γ.

Ймовірність того, що інтервал  містить в собі невідомий параметр Q, дорівнює γ. Довірчим називають інтервал , що покриває невідомий параметр із заданою надійністю γ.

4.6.1 Довірчий інтервал для оцінки  математичного сподівання  нормального розподілу при невідомому s

Нехай кількісна ознака Х генеральної сукупності розподілена нормально і s невідоме. Побудуємо випадкову величину 

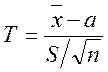,                                           (4.1)

яка має розподіл Стьюдента  з k=n-1 ступенями вільності, де  а – математичне сподівання;  - середнє значення; S - стандартне відхилення.

Визначимо значення t_g  з рівняння

,                        (4.2)

де g – задана надійність. визначаємо за допомогою таблиці, або  функції Excel  = СТЬЮДРАСПОБР (1- γ; n-1).

Підставимо значення Т (4.1) в рівняння (4.2). Отримаємо

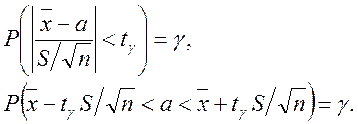
Користуючись розподілом Стьюдента, ми знайшли довірчий інтервал , що покриває невідомий параметр а з надійністю γ.

Приклад. За даними 9 незалежних вимірювань фізичної величини знайдене =42,319 і величини  S=5,0. Оцінити істинне значення вимірюваної величини  з надійністю γ=0,95.

Істинне значення вимірюваної величини дорівнює математичному сподіванню, тому задача зводиться до оцінки математичного сподівання при невідомому σ за допомогою довірчого інтервалу:

,

який покриває a із заданою надійністю γ=0,95. Використовуючи СТЬЮДРАСПОБР(1-0,95; 9-1), знаходимо, щоt_r=2,3,

=2,31* =3,85.

Отже, довірчий інтервал, що з надійністю γ=0,95 покриває істинне значення  вимірюваної величини:

38,469< a <46,169.

Для n=25, t_γ =2,09, отже довірчий інтервал, що з надійністю γ=0,95 покриває істинне значення  вимірюваної величини  

42,319 – 3,48< a <42,319 + 3,48 ,