Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 4

Геометрично це рівняння можна пояснити таким чином: F(x) є ймовірність того, що випадкова величина X набере значення, що зображується на числовій осі точкою, що лежить ліворуч точки х, тобто  випадкова точка X потрапить в інтервал (- ∞,x), див. рис. 2.2.

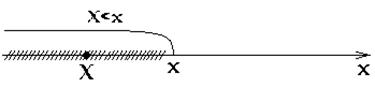
Рисунок 2.2 – Геометрична  інтерпретація функції розподілу

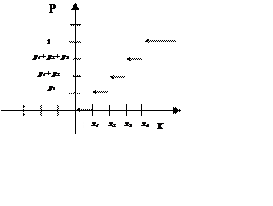
Рисунок 2.3 – Функція розподілу (графічне подання)

Властивості:

1  0 ≤ F(x) ≤ 1,   F(x) – неспадна обмежена функція;

2  F(x) – монотонно зростає на R: a < b   → F(a) ≤ F(b););

3  F(x)- неперервна ліворуч на R.

4  F(-¥)=0;        F(+¥)=1;

5  Ймовірність того, що XÎ[a, b)       P(a ≤ X < b) = F(b) – F(a).

{Х<b}

{X < а}          {а ≤ X < b}

Рисунок 2.4 – Геометрична  інтерпретація обчислення

ймовірності того, що випадкова величина набере значення з інтервалу [a, b)

2.1.2 Закон розподілу неперервної випадкової величини

Найважливішою характеристикою неперервної випадкової величини (крім функції розподілу) є щільність розподілу ймовірностей. Випадкова величина X називається неперервною, якщо її функція розподілу неперервна й диференційована на інтервалі [a, b], крім, можливо, окремих точок.

Щільністю розподілу ймовірностей (щільністю розподілу, щільністю ймовірностей або просто щільністю) неперервної випадкової величини X називається похідна її функції розподілу.

Позначається щільність розподілу неперервної випадкової величини X через f(x).

Таким чином, за визначенням

f(x) =F'(x).

Функцію f(x) називають також диференціальною функцією розподілу; вона є однією з форм закону розподілу випадкової величини,  існує тільки для неперервних випадкових величин.

Щільність розподілу має такі властивості:   

·  f(x) невід’ємна, тобто ;

·  функція розподілу неперервної випадкової величини X може бути обчислена через її щільність імовірності за формулою

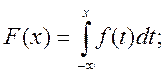
·  умова нормування: невласний інтеграл від щільності ймовірності неперервної випадкової величини X у нескінченних межах дорівнює одиниці, тобто

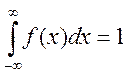
·  ймовірність влучення неперервної випадкової величини X у проміжок [а; b] дорівнює визначеному інтегралу від її щільності в межах від а до b, тобто

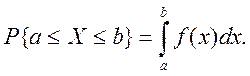
Геометрично ця ймовірність дорівнює площі S фігури, обмеженої зверху кривою розподілу f(x), що  опирається на відрізок [а; b] (рис. 2.5).

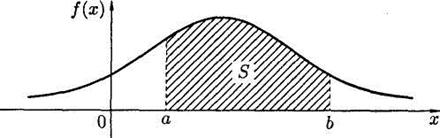
Рисунок 2.5 – Геометрична  інтерпретація ймовірності попадання неперервної випадкової величини X у проміжок [а; b]

2.2. Числові  характеристики  випадкових  величин

Скласти повне уявлення про випадкові величини тільки за законом розподілу  часто буває досить важко. Тому виникає необхідність характеризувати  випадкову величину за допомогою деяких сталих величин, отриманих  на  основі їх закону розподілу. 

До важливих числових характеристик відносять математичне сподівання і дисперсію, середнє квадратичне відхилення, моду, медіану.

2.2.1 Математичне сподівання

Математичним сподіваннямдискретної випадкової величини X, яка має закон розподілу

р_i = Р{Х = x_i}, i= 1,2,3,..., n,

нази­вають число, що дорівнює сумі добутків значень випадкової величини на відповідні ймовірності.

Математичне сподівання позначається через MX (або М(Х)).

Таким чином, за визначенням

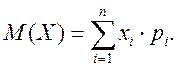
Якщо кількість можливих  значень випадкової величини X нескінченна (зліченна), то

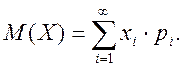
При цьому вимагаємо абсолютної збіжності ряду.

Ймовірнісний зміст математичного сподівання.

Нехай зроблено n випробувань і випадкова величина Х набрала m₁  раз значення x₁, m₂ разів – x₂ ,..., m_к – x_к .    

Середнє арифметичне значення ,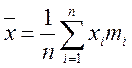

де .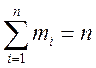

При великій кількості випробувань (n → ∞) математичне сподівання наближено дорівнює середньому арифметичному значенню  М(X).

Математичним сподіванням неперервної випадкової величини X із щільністю розподілу f(x)  називається число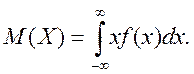

Властивості математичного сподівання:

1 Математичне сподівання постійної (C=const) дорівнює самій постійній

M(С) = С.

2 Постійний множник виноситься за знак математичного сподівання