Аналіз даних: Навчальний посібник (Розділи: Предмет курсу. Основні задачі. Випадкові величини. Нормальний розподіл і основні розподіли, пов'язані з ним), страница 23

Двухвыборочный t-тест с одинаковыми дисперсиями
	Переменная 1	Переменная 2
Среднее	3	4
Дисперсия	2,5	2,5
Наблюдения	5	5
Объединенная дисперсия	2,5
Гипотетическая разность средних	0
df	8
t-статистика	-1
P(T<=t) одностороннее	0,173296754
t критическое одностороннее	1,85954832
P(T<=t) двухстороннее	0,346593507
t критическое двухстороннее	2,306005626

Як видно з таблиці, Excel дозволяє отримати всю необхідну інформацію для розв’язання поставленої задачі. Пояснимо, що df–  кількість ступенів вільності, t-статистика – розраховане значення t_р, tкритическое одностороннее – відповідно , t критическое двухстороннее – t_{двост. кр.}.

Обираємо t критическое двухстороннее – для випадку 1, t критическое одностороннее – для випадків 2 та  3.

Приклад. Є мережа аптек. Протягом місяця проводилася реклама препарату. Необхідно перевірити гіпотезу про те, що середнє  збільшення реалізації в аптеках при рекламуванні перевищує 3000 грн із рівнем значущості α=0,05.

            Обсяг реалізації за місяць, тис.грн

	1	2	3	4	5	6	7	8
До реклами	13	23	12	11	24	34	32	18
Після реклами	20	24	11	17	28	34	39	24

1  Перевірити, чи можна вважати значення розподілів нормальним. Будемо використовувати наближений критерій 

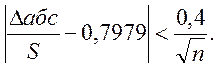
Обчислюємо:

=20,875,      =24,625,

Δабс₁=7,375,(СРОТКЛ(<діапазон>),

 Δабс₂=6,78,

 

 

Перевіряємо умову

<  ,     

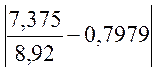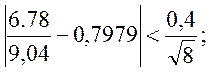
      0,029<0,14 ,                       0,048<0,14.

Умови виконуються, отже, вибірки підкоряються нормальному закону розподілу.

2    Перевіряємо гіпотезу про рівність дисперсій:

   

F_кр  знаходимо з рівняння ; α/2=0,025.

Використовуємо Сервис – Анализ данных – Двухвыборочный F-тест.

Отримаємо такі дані:

Двухвыборочный F-тест для дисперсии
	Переменная 1	Переменная 2
Среднее	24,625	20,875
Дисперсия	81,69642857	79,55357143
Наблюдения	8	8
df	7	7
F	1,026936027
P(F<=f) одностороннее	0,48646589
F критическое одностороннее	4,99

F_p = 1,0269 , F_кр= 4,99 . Оскільки F_p < F_кр , приймаємо гіпотезу Н₀,  дисперсії рівні.

            3 Використовуючи Сервис – Анализ данных– Двухвыборочный t-тест з одинаковыми дисперсиями, перевіряємо гіпотези

H₀:  =  -3;  H₁: ≠ -3. 

Двухвыборочный t-тест с одинаковыми дисперсиями
	Переменная 1	Переменная 2
Среднее	20,875	24,625
Дисперсия	79,55357143	81,69642857
Наблюдения	8	8
Объединенная дисперсия	80,625
Гипотетическая разность средних	3
df	14
t-статистика	0,167
P(T<=t) одностороннее	0,077467216
t критическое одностороннее	1,76
P(T<=t) двухстороннее	0,154934432
t критическое двухстороннее	2,145

Як бачимо з таблиці t _p=0,167, t _{кp.двост}=2,145. Оскільки t_p< , то середні значення рівні.

Висновок. Можна вважати, що середній обсяг реалізації збільшився на 3 тис. грн.

5.5.2 Перевірка гіпотези про рівність середніх при
нерівних дисперсіях (малі вибірки)