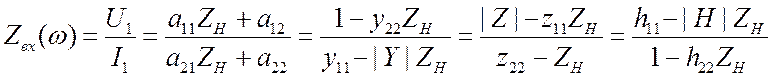 . (3.20)
. (3.20)
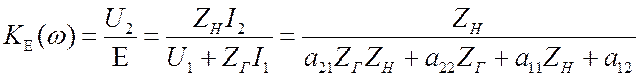 .
(3.21)
.
(3.21)
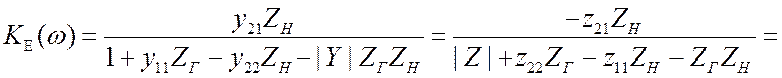
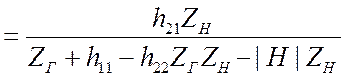 .
. ![]() .
(3.21)
.
(3.21)
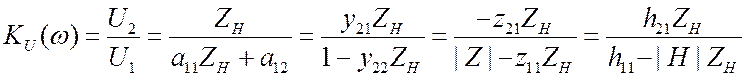 . (3.22)
. (3.22)
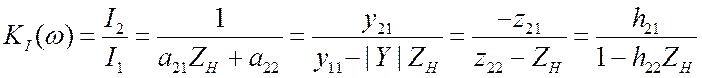 .
(3.23)
.
(3.23)
Для определения выходного сопротивления воспользуемся формулой (3.4).
![]() .
. 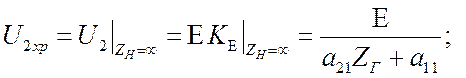
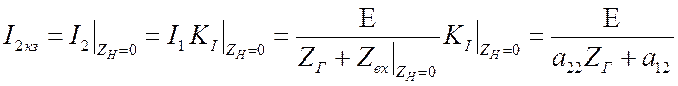 . В итоге:
. В итоге:
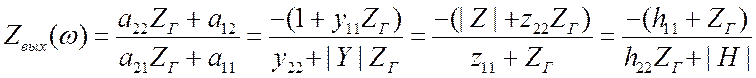 . (3.24)
. (3.24)
Приведённые формулы широко используются. Для многих простых типовых 4 х-пол. элементы матриц уже вычислены и приводятся в учебниках и справочниках. Нужно брать готовые формулы и подставлять в них конкретные значения сопротивлений.
3.6.6. Примеры вычисления элементов матриц.
Поскольку элементы матриц
не зависят от токов и напряжений, от сопротивлений генератора и нагрузки, то
для вычисления элементов матриц выбирают наиболее простые режимы работы 4
х-пол. Это холостой режим (хр), ![]() , и
режим короткого замыкания (кз),
, и
режим короткого замыкания (кз), ![]() , на выходе или на
входе. Приведём несколько примеров.
, на выходе или на
входе. Приведём несколько примеров.
1. Простой делитель, рис.
3.25а. Рассмотрим два режима и определим элементы матрицы ![]() .
. ![]() .
.
а). Режим короткого замыкания на выходе, рис. 3.25б.
![]() .
.![]() . Тогда:
. Тогда: ![]() .
.
б). Холостой режим на выходе, рис. 3.25а. ![]() .
. ![]() ;
;
![]() .
. ![]() .
.
В итоге 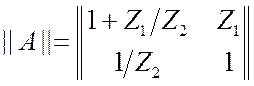 .
(3.25)
.
(3.25)
![]() , как и должно быть.
, как и должно быть.
2. Т – образный 4 х-пол.,
рис 3.18а. Его можно представить в виде каскадного соединения двух более
простых, рис. 3.26. Для первого мы только что вычислили матрицу ![]() . Второй есть частный случай первого, если
. Второй есть частный случай первого, если ![]() (
(![]() заменяется на
заменяется на ![]() ). Таким образом, имеем:
). Таким образом, имеем: 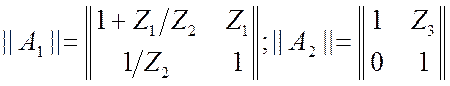 . Общая матрица
. Общая матрица 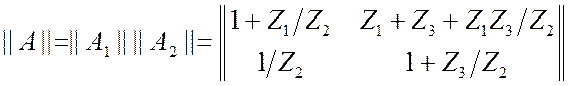 .
(3.26)
.
(3.26)
Приведём без вывода другие матрицы этого 4 х-пол. Получите их
самостоятельно. 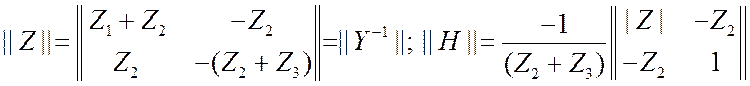 . (3.26а) Матрица сопротивлений
оказывается проще других.
. (3.26а) Матрица сопротивлений
оказывается проще других. ![]() .
.
3. П – образный 4 х-пол.,
рис. 3.18б. Матрицу ![]() легко получить таким же
способом, как в предыдущем примере. Сделайте это в качестве упражнения.
легко получить таким же
способом, как в предыдущем примере. Сделайте это в качестве упражнения. 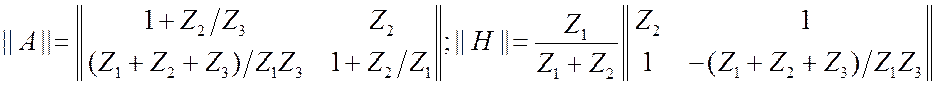 . Матрица
. Матрица ![]() записывается
проще, если ввести проводимости элементов
записывается
проще, если ввести проводимости элементов ![]() . Тогда
. Тогда
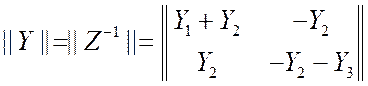 .
.
4. Два звена делителя, рис. 3.27. Напишем только
матрицу ![]() .
.
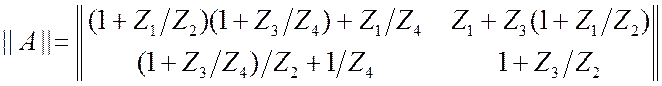 .
(3.27)
.
(3.27)
5. «Мостовой» 4 х-пол., рис. 3.28.
Приведём тоже только матрицу ![]() .
.
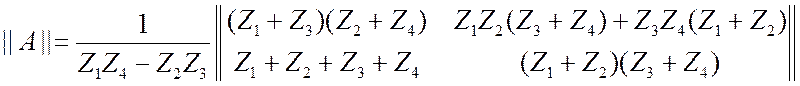 . (3.28)
. (3.28)
Условие ![]() есть условие «баланса»
моста. При этом
есть условие «баланса»
моста. При этом ![]() .
.
Рассмотрим ещё три примера специфических 4 х-пол.
6. Просто провода, рис.
3.29. ![]() . Такой 4 х-пол. ничего не
меняет, и является частным случаем первого примера, когда
. Такой 4 х-пол. ничего не
меняет, и является частным случаем первого примера, когда ![]() , а
, а ![]() . Матрицы
. Матрицы
![]() и
и ![]() для
него не существуют.
для
него не существуют. ![]() . Если провода перекрестить, то
изменится знак у элементов.
. Если провода перекрестить, то
изменится знак у элементов. ![]() .
.
7. «Разорванный» 4 х-пол.,
рис. 3.30. ![]()
![]() . У него нет связи
между входом и выходом, поэтому матрица
. У него нет связи
между входом и выходом, поэтому матрица ![]() для
этого 4 х-пол. не существует. Проще всего найти матрицу
для
этого 4 х-пол. не существует. Проще всего найти матрицу ![]() .
. ![]() . С помощью
такого 4 х-пол. можно сделать регулярным любое соединение 4 х-пол.
. С помощью
такого 4 х-пол. можно сделать регулярным любое соединение 4 х-пол.
8. Идеальный
трансформатор, рис. 3.31. Пусть ![]() есть коэффициент
трансформации. Тогда:
есть коэффициент
трансформации. Тогда: ![]() . Матрицы
. Матрицы ![]() и
и
![]() для него не существуют.
для него не существуют.
3.6.7. Характеристические параметры обратимого 4 х-пол.
Элементы любой из
рассмотренных матриц дают некоторую систему параметров, однозначно и полностью
характеризующую 4 х-пол. и позволяющую определить все его
характеристики (![]() и пр.).
и пр.).
Часто между генератором и
нагрузкой оказывается 4 х-пол. (фильтр, усилитель, линия передачи,
корректирующие цепи), рис. 3.14. Это очень типичная ситуация. В определённой
полосе частот мы хотим передать сигнал в нагрузку с минимальными потерями, с
минимальным ослаблением. Возникает вопрос, каково должно быть ![]() , чтобы реализовать это условие для
определённого
, чтобы реализовать это условие для
определённого
4 х-пол.? Перечисленные уже системы параметров не дают чёткого
ответа на поставленный вопрос.
В теории цепей вводят ещё
особую систему параметров 4 х-пол., не привязанную однозначно к
какой-либо системе уравнений. Эти параметры и называют характеристическими. Они
позволяют получить ответ на поставленный вопрос. Для пассивного (обратимого) 4
х-пол. независимыми являются три параметра, три элемента матриц. Поэтому
и вводят три новых параметра. Два характеристических сопротивления, 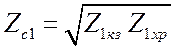 и
и 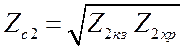 , и
характеристическую постоянную передачи
, и
характеристическую постоянную передачи 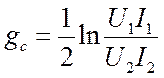 , при
условии, что
, при
условии, что ![]() . Здесь:
. Здесь: ![]() и
и
![]() есть входные сопротивления 4 х-пол.
для режимов короткого замыкания и холостого хода на выходе;
есть входные сопротивления 4 х-пол.
для режимов короткого замыкания и холостого хода на выходе; ![]() и
и ![]() - это
сопротивления 4 х-пол. со стороны выхода, при обратном направлении
передачи, когда на входе реализуются режимы короткого замыкания и холостого
хода. Такую ситуацию мы рассматривали. Входное сопротивление 4 х-пол.
со стороны выхода при обратном направлении передачи есть выходное
сопротивление.
- это
сопротивления 4 х-пол. со стороны выхода, при обратном направлении
передачи, когда на входе реализуются режимы короткого замыкания и холостого
хода. Такую ситуацию мы рассматривали. Входное сопротивление 4 х-пол.
со стороны выхода при обратном направлении передачи есть выходное
сопротивление.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.