Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 17

В отличие от полосового фильтра, здесь начало переходной  характеристики () определяется ФВЧ, а затем начинает проявлять себя ФНЧ. Скачок напряжения на входе при  воспроизводится полностью за счёт ФВЧ, в то время как постоянная составляющая возникает за счёт ФНЧ.

Интересно определить реакцию РФ на длинный радиоимпульс с частотой заполнения , равной частоте режекции (). Воспользуемся преобразованием Лапласа (). Пусть . Спектр такого сигнала мы уже вычисляли, формула (2.19). Тогда . 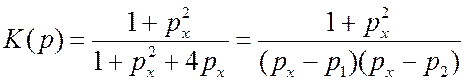, где  и  - корни характеристического уравнения. . В итоге (): 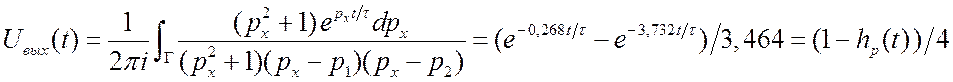. Результат приведён на рис. 3.58. Пунктиром на рис. изображена часть . Такой процесс появится на выходе РФ при включении длинного радиоимпульса (аналогичный будет и при выключении). Никаких осцилляций нет, если фильтр точно настроен на частоту сигнала. При неточной настройке, на изображённый сигнал будут наложены колебания, амплитуда которых будет расти по мере увеличения расстройки.

3.8.10.  Неискажающая цепь. Особенности поведения .

Мы рассмотрели примеры различных  цепей и накопили достаточный материал для обсуждения особенностей поведения модуля и аргумента коэффициента передачи.  есть дробно-рациональная функция частоты, отношение двух полиномов. При этом полином в числителе не может иметь степень бóльшую, чем в знаменателе, поскольку  должен быть ограничен, когда . На самом деле, для реальных цепей реализуется более жёсткое условие; , когда . Слово ограничен относится только к идеализированным цепям, типа дифференцирующей.

Нетрудно представить себе коэффициент передачи  идеальной цепи, не искажающей сигнал. Очевидно, цепь должна одинаково пропускать все частоты (весь спектр входного сигнала), т.е. . Как должна себя вести фазовая характеристика? Она должна быть линейной функцией частоты с отрицательным наклоном. . Величина  имеет смысл времени задержки (запаздывания) сигнала. В самом деле, пусть  есть спектр сигнала на входе цепи. Тогда , а выходной сигнал .

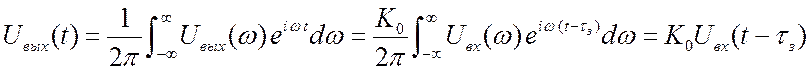Сигнал на выходе цепи получился не искажённым, но задержанным на время . Неискажающая цепь есть идеализация. Любая реальная цепь искажает сигнал, причём искажения могут возникать за счёт неидеальности как амплитудной, так и фазовой характеристик.

Сформулируем теперь общую закономерность поведения фазовой характеристики реальных цепей. По аналогии с физическими системами величину  называют временем группового запаздывания. Если , то это нормально, значит мы имеем нормальный характер поведения (нормальная дисперсия). Это мы и видели на примерах фильтров НЧ. ВЧ и полосовых. Может быть аномальное поведение ? Да, может. Пример с РФ это иллюстрирует. Если , то на этой частоте получается скачок фазы на  (вверх). В противном случае, изменение фазы вблизи частоты режекции будет непрерывным, с аномальной зависимостью (). Однако, аномальная зависимость имеет место только в окрестности  (линия или полоса поглощения в физической системе).

Для идеальной неискажающей цепи  постоянно, и следовательно, функция , когда . Для реальных цепей  существенно зависит от частоты. Например, для интегрирующей цепи:  , когда . Последняя тенденция справедлива, фактически, для любой реальной цепи, поскольку в таких цепях набег фазы ограничен.

3.9.  Примеры цепей. Цепи с индуктивностями.

Такие цепи позволяют получить фильтры лучшего качества, чем  цепи. Мы уже рассматривали последовательный и параллельный колебательные контуры, как двухполюсники, и анализировали их сопротивление. Теперь рассмотрим ситуацию, когда они образуют четырёхполюсник. Начнём с последовательного колебательного контура.

3.9.1.  Последовательный колебательный контур.

Чаще всего выходное напряжение снимается с конденсатора, как изображено на рис. 3.59а. Примем  (включено в ). Напомним характерные параметры контура и переменные:  есть резонансная частота,  есть безразмерная (относительная) частота, характеристическое сопротивление , добротность , затухание , абсолютная расстройка , относительная расстройка , обобщённая расстройка , если .