Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 16

В заключение, на рис. 3.54, изображены качественно типичные искажения прямоугольного импульса длительности  в широкополосном ПФ. Рисунки получены путём наложения двух реакций  на передний и задний фронты импульса. Первым изображён случай малых искажений импульса, который реализуется при условии . В этом случае процессы заряда и разряда конденсаторов цепи очень чётко прослеживаются.

Если по-прежнему , но сравнимо с , например, , то будут наблюдаться сильные искажения импульса, рис. 3.54б. Процесс протекает как в интегрирующей цепочке. Конденсатор  не успевает зарядиться, и дифференцирующая цепочка практически себя не проявляет. Если длительность импульса становится сравнима с  (например ), то опять импульс будет сильно искажён, но теперь уже за счёт дифференцирующей цепи, рис. 3.54в. Влияние интегрирующей цепи мало заметно при таком временном масштабе, но оно всегда есть, сигнал  непрерывен.

3.8.8.  Режекторный RC фильтр. Двойная Т – образная цепь.

Схема фильтра изображена на рис. 3.55. Цепь симметрична, и образована параллельным включением по входу и выходу двух простых Т – образных цепей. При параллельном соединении таких цепей «регулярность» соединения не нарушается, поэтому общая матрица проводимости получается сложением матриц отдельных Т – образных цепей. Будем, для простоты, считать . Тогда коэффициент передачи цепи . Только эти два элемента общей матрицы нам надо определить.

Т – образный 4 ^х – пол. мы уже рассматривали. Он изображён на рис. 3.18а, а элементы матрицы  приведены в выражении (3.26). Для симметричного () 4 ^х – пол. нужные нам элементы таковы: ; . Тогда для первой простой цепи с двумя сопротивлениями в продольной ветви будем иметь: ; ; . Для второй цепи, с двумя конденсаторами: ; . Складывая соответствующие элементы обеих матриц, найдём интересующие нас элементы общей матрицы  и . ;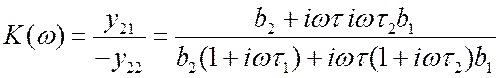. Получилось сложное выражение (отношение двух кубичных полиномов). Но его можно упростить, положив  (это не делает цепь хуже, наоборот, улучшает). Тогда , и этот общий множитель можно сократить. В результате:

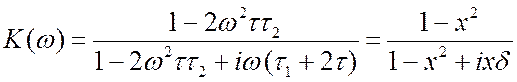.                                               (3.51) Здесь: . Условие  записывают иначе, введя параметр . Тогда: ; . Особенность поведения коэффициента передачи заключается в том, что, когда  или  (идеализированная цепь).  при , т.е.  и есть частота режекции. Режекция в данной цепи получается за счёт сложения двух противофазных напряжений одинаковой амплитуды.

Легко показать, решив уравнение , что полоса режекции на уровне 0,71, . Минимальное  получается, когда . Тогда: . Характеристики для этого случая приведены на рис. 3.56. Режекторный фильтр получился широкополосным, низкого качества. На частоте режекции происходит скачок фазы на  вверх (при условии, что ). Если цепь не настроена точно (не выполнено условие ), то  не обратиться в ноль на частоте режекции, а  будет меняться плавно, непрерывно. Эта ситуация изображена на рис. 3.56 качественно, пунктиром.

Если использовать логарифмический масштаб по оси частот, то характеристики будут более симметричными относительно частоты режекции.

3.8.9.  Переходные процессы в режекторных фильтрах.

Ранее мы убедились в том, что коэффициент передачи широкополосного полосового фильтра можно приблизительно представить в виде произведения коэффициентов передачи дифференцирующей и интегрирующей цепочек (каскадное их соединение). При этом граничная частота ФНЧ оказывается значительно больше, чем для ФВЧ.

Примем  (, минимальная полоса режекции). Коэффициент передачи рассмотренного РФ точно получается сложением коэффициентов передачи двухзвенных фильтров НЧ и ВЧ (что в некотором смысле соответствует их параллельному соединению без взаимного влияния). Но теперь граничная частота ФНЧ значительно ниже, чем для ФВЧ (). На основании этих соображений легко можно представить качественно переходную характеристику РФ. Мы не вычисляли характеристики цепей для , но для качественных рассуждений можно использовать уже приведённые на рис. 3.50 и 3.52 для . Представим их на одном рисунке и сложим. Получим скачок, потом быстрое убывание и, наконец, медленный рост к предельному значению, равному единице. Качественные соображения прекрасно работают. Всё так и будет. Если бы мы имели  двухзвенных цепей при , мы получили бы точный результат, изображённый на рис. 3.57 (получите его самостоятельно). .