Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 20

Теперь учтём полюса коэффициента передачи. . . 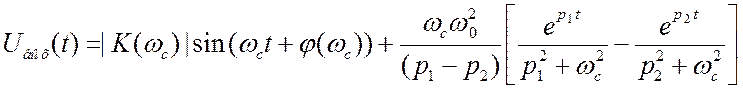Напишем результат приближённо, считая . При этом . В итоге будем иметь ():.                           (3.56) Множитель в скобках определяет изменение амплитуды и является огибающей процесса установления, рис. 3.65. Огибающая меняется как переходная характеристика интегрирующей цепи с постоянной времени . Амплитуда устанавливается до уровня 0,9 стационарного значения за время .

Существуют приближенные методы, которые позволяют сразу находить огибающую процесса, не интересуясь деталями высокочастотного заполнения. При этом коэффициент передачи, в окрестности резонансной частоты, записывают не как функцию частоты , а как функцию расстройки .  (). Это очень похоже на коэффициент передачи интегрирующей цепи.

Если контур не настроен точно на частоту сигнала, но расстройка мала, то установление амплитуды к стационарному значению происходит не монотонно, а с медленными осцилляциями (биения частот  и ).

Приведённые результаты позволяют получить качественные картинки искажений длинного радиоимпульса с прямоугольной огибающей настроенным контуром с большой добротностью. При выключении сигнала произойдёт медленное уменьшение амплитуды с той же временной постоянной. Изменение огибающей выглядит так, как на рис. 3.37 для интегрирующей цепи.

3.9.6.  Параллельный колебательный контур.

Схема изображена на рис. 3.66а. Будем считать добротность контура . Тогда, как мы выяснили (формула 3.7), параллельный контур имеет большое входное сопротивление и оно максимально при резонансе. . Это обстоятельство и определяет особенности применения параллельного контура. Если мы хотим иметь контур с большой добротностью, то сопротивление генератора должно быть много больше, чем . В противном случае, при подключении генератора, добротность уменьшится значительно, поскольку сопротивление генератора шунтирует контур. Так, если , то добротность уменьшится в два раза.

Обычно, для анализа схем с параллельным контуром используется генератор тока , где  есть крутизна генератора, рис 3.66б. Далее, схему упрощают, пересчитывая сопротивление генератора в контур, рис. 3.66в. При этом . Теперь , но в выражение для  надо вместо  подставить . Тогда .               (3.57)
Здесь: . Нас интересует поведение коэффициента передачи вблизи резонансной частоты, . В числителе выражения для  стоит мало меняющаяся функция . По-прежнему всё определяет выражение  в знаменателе, такое же, как и для последовательного контура. Следовательно, зависимость  практически не изменится, а  нужно скорректировать, добавив , поскольку на резонансной частоте сопротивление контура активно.

Таким образом, и последовательный, и параллельный контур с большой добротностью являются типичными узкополосными полосовыми фильтрами. Разница только в сопротивлениях; у последовательного контура сопротивление маленькое, у параллельного – большое.

Можно и в этом случае всё свести к последовательному контуру на уровне схем. В самом деле, активный двухполюсник с генератором тока на рис. 3.66в надо заменить эквивалентным генератором напряжения, как на рис. 3.66г. Тогда: . Для коэффициента передачи мы снова получим выражение (3.57).

В реальных схемах для улучшения согласования с сопротивлениями генераторов часто используют неполное включение контура. Анализ сопротивления контура при таком включении был проведён в разделе двухполюсников, рис. 3.13.

3.9.7.  Связанные контура.

Рассмотренные примеры показали, что использование простого колебательного контура с большой добротностью даёт нам узкополосный полосовой фильтр, но низкого качества. Задав резонансную частоту и полосу пропускания, мы однозначно определяем коэффициент передачи контура, и изменить уже ничего не можем. Наиболее эффективный способ улучшения качества фильтров состоит в усложнении колебательной системы. Тогда появляются новые параметры, новые возможности, позволяющие улучшить избирательность фильтров.