Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 2

Это очень важная и полезная теорема теории цепей. Она позволяет заменить сложный активный двухполюсник эквивалентным генератором напряжения с указанными параметрами и перейти к простой схеме, изображённой на рис. 3.3б. Теоремой часто пользуются для эквивалентных преобразований цепи, для упрощения цепи.

Для доказательства теоремы включим последовательно с нагрузкой два одинаковых идеальных генератора с ЭДС  и  противофазно (очень распространённый приём в теории цепей), как на рис. 3.3а. В цепи ничего не изменится. Цепь линейна. Рассмотрим отдельно два режима. Результат получится их наложением.

1. Пусть . Работают все внутренние источники и . Подберём  так, чтобы исчез ток через нагрузку. Ток за счёт внутренних источников компенсируется током за счёт . Падения напряжения на нагрузке не происходит, . При этом можно считать, что реализован режим холостого хода, и цепь  как бы разомкнута. Каково должно быть , чтобы реализовать эти условия? Ответ: .

2. Теперь выключим все внутренние источники и . Остаётся . Какой ток будет течь в нагрузке? Ответ очевиден. 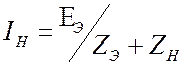 ,  где  есть сопротивление пассивного двухполюсника.

Включаем все источники. Суммарный ток в нагрузке останется таким же. Это и есть искомый ток. Теорема доказана. Отметим, что параметры эквивалентного генератора не зависят от сопротивления нагрузки.

Эквивалентное сопротивление генератора можно выразить иначе. Пусть . Тогда ток короткого замыкания 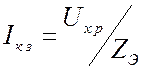. Отсюда 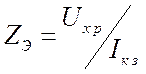. (3.4) Сопротивление эквивалентного генератора равно отношению напряжения холостого режима к току короткого замыкания. Этот результат широко используется при анализе цепей.

Активный линейный двухполюсник можно заменить и эквивалентным генератором тока , рис. 3.3в. При этом , а  одинаково для обоих генераторов.

3.3.  Передача мощности от генератора к нагрузке. Согласование.

Схема цепи изображена на рис. 3.4. Сопротивления генератора и нагрузки комплексны (). Ток в цепи . Сопротивление генератора считается заданным. Рассмотрим среднюю активную мощность в нагрузке и определим условие оптимальной передачи мощности.

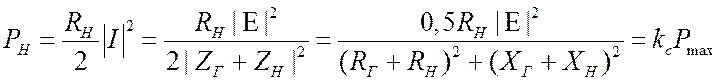.                   (3.5)
Здесь 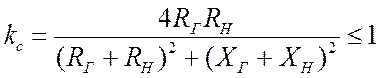 есть коэффициент согласования или коэффициент передачи мощности.  только при условии согласования, когда  (). есть максимальная мощность, которая может быть передана в нагрузку при условии согласования. При этом такая же мощность выделяется и в генераторе. Это важное обстоятельство надо учитывать.

3.4.  Линейные пассивные двухполюсники.

Любая ветвь сложной цепи является двухполюсником (будем писать 2^х-пол.). Пусть  и  есть комплексные амплитуды напряжения на 2^х-пол. и протекающего через него тока, на определённой частоте . Происходящие внутри 2^х-пол. процессы нас не интересуют. Тогда все особенности линейного пассивного 2^х-пол. полностью определяются одним комплексным параметром, его сопротивлением , какой бы сложной не была структура 2^х-пол. Реальную и мнимую части ,  и , называют активной и реактивной составляющими комплексного сопротивления. Сформулируем некоторые определения.

1. Если два 2^х-пол. обладают одинаковыми сопротивлениями , то они эквивалентны для внешней цепи. Один можно заменить другим.

2. Если , где  (вещественно), то 2^х-пол. с сопротивлениями  и  называются подобными. Например, две индуктивности  и .

3. Если , то 2^х-пол. с сопротивлениями  и  называются обратными. Например, индуктивность и ёмкость. .

4. Если на некоторой частоте  реактивная составляющая сопротивления , то  есть резонансная частота 2^х-пол.

Приведём  несколько примеров эквивалентных 2^х-пол., изображённых на рис. 3.5. Эти примеры предлагается рассмотреть самостоятельно в качестве упражнений. Надо вычислить сопротивления эквивалентных 2^х-пол. и приравнять их для произвольных значений  и . Ответы для этих примеров следующие:

а. .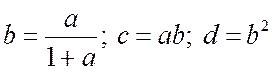

б. .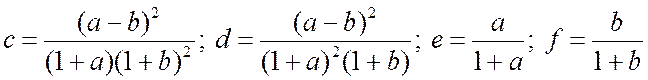

в. .

Можно получить и условия эквивалентности при переходах правых 2^х-пол. в левые. Три цепи на рис. 3.6, содержащие обратные 2^х-пол., эквивалентны простому 2^х-пол. с одним сопротивлением . Покажите это самостоятельно.

3.4.1. Типичная задача для 2^х-пол.