Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 11

Все фильтры делятся на четыре типа, в зависимости от того, какие частоты они пропускают. На рис. 3.32 приведены качественные зависимости  для идеальных фильтров. Фильтры нижних частот (ФНЧ) пропускают частоты ниже , а частоты  подавляют (сильно ослабляют). Фильтры верхних частот (ФВЧ), наоборот, пропускают частоты , а нижние подавляют. Полосовые фильтры (ПФ) пропускают полосу частот от  до . Частоты вне этой полосы подавляются. Если  (некая средняя частота), то фильтр называют узкополосным. В противном случае – широкополосным.  Режекторные (заградительные) фильтры (РФ) подавляют сигналы в полосе частот от  до . Частоты вне этой полосы пропускаются фильтром. Режекторные фильтры тоже могут быть узкополосные и широкополосные.

Фильтры с указанными идеализированными характеристиками нереализуемы. Это мы покажем позже. Дальнейшие особенности реальных фильтров и терминологию мы обсудим на примере ФНЧ, типичная характеристика которого изображена на рис. 3.33. Различают не два, а три частотных интервала, определяемые двумя заданными уровнями, например  и 0,1. Частоты ниже  фильтр пропускает, т.к. в этой полосе , близок к единице. Частоты выше  фильтр не пропускает (условно), поскольку значительно их ослабляет (на порядок, при заданном уровне 0,1). Это полоса режекции. Интервал от  до  называют переходной областью. Чем она ýже, тем лучше, качественнее фильтр.

Для количественной оценки качества фильтра чаще всего используют два критерия. 1. Задают ослабление, вносимое фильтром, при заданном изменении частоты относительно граничной. Например, фильтр ослабляет сигнал в 10 раз на частоте . 2. Качество характеризуют коэффициентом «прямоугольности» . Для идеального ФНЧ , для реального – меньше.

Приведём пример и оценим качество полосового фильтра в хорошем приёмнике сигнала с амплитудной модуляцией. Пусть приёмник настроен на частоту . Все частоты, находящиеся в полосе  кгц, приёмник должен пропускать, т.е.  кгц. При расстройке на 10 кгц от частоты , усиление приёмника должно уменьшиться в 100 раз (40 децибелл). Примем  кгц. Тогда . Это уже фильтр хорошего качества.

Этими сведениями о фильтрах мы пока и ограничимся. Перейдём к рассмотрению примеров.

3.8.  Примеры различных цепей.

Будем в первую очередь интересоваться стационарными характеристиками цепей, и прежде всего, коэффициентом передачи, поскольку он связывает входное напряжение и выходное. При этом для упрощения анализа, будем считать генератор идеальным (), а  (холостой режим). Ранее были приведены общие формулы, позволяющие учесть сопротивления генератора и нагрузки. Часто эти сопротивления могут быть учтены и в самом 4 ^х - пол.

3.8.1. Интегрирующая цепь. Элементарный ФНЧ.

Варианты цепи изображены на рис. 3.34. Коэффициенты передачи этих двух цепей одинаковы. Простые вычисления для  цепи дают:

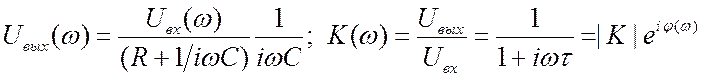.                  (3.40)

Здесь  ( для цепи с индуктивностью) есть постоянная времени цепи.  определяет изменение амплитуды гармонического сигнала, а аргумент  - сдвиг фазы выходного напряжения относительно входного. Зависимости этих величин от частоты тоже изображены на рис. 3.34.

Если , то , а это есть оператор интегрирования. Вот почему цепочку называют интегрирующей. В определённых частотных и временных интервалах сигнал на выходе цепочки будет пропорционален интегралу от входного сигнала.

Интегрирующая цепочка представляет типичный ФНЧ, но очень плохой,  всего 0,1. Переходная область в 9 раз шире, чем полоса пропускания.

Перейдём к анализу переходной характеристики. Её мы вычисляли во вводной части курса. Если , то . Получите теперь этот результат самостоятельно, пользуясь преобразованием Фурье или Лапласа. Он изображён на рис. 3.35. Когда ,  (разлагаем экспоненту в ряд). Вот вам и интегрирование. Чем больше , тем больше промежуток времени, в котором осуществляется интегрирование. Когда , . Время нарастания сигнала от нуля до значения, равного 0,9 от установившегося, называют длительностью фронта сигнала. Можно решить соответствующее уравнение  и получить результат, .