Генератор напряжения с
ЭДС ![]() и сопротивлением
и сопротивлением ![]() нагружен
на 2х-пол. ЭДС задано. Требуется найти ток в цепи (или ток задан, а
требуется найти напряжение). Существуют два типичных варианта решения этой
задачи.
нагружен
на 2х-пол. ЭДС задано. Требуется найти ток в цепи (или ток задан, а
требуется найти напряжение). Существуют два типичных варианта решения этой
задачи.
Первый вариант классический. Составляется дифференциальное уравнение этой цепи (или система уравнений в более сложной ситуации) и оно решается относительно тока. Такой пример уже был рассмотрен во вводной части.
Второй называют спектральным методом. Он содержит следующие этапы.
1. Предполагая
зависимость от времени ![]() , находим комплексные сопротивления
2х-пол. и генератора,
, находим комплексные сопротивления
2х-пол. и генератора, ![]() и
и ![]() .
.
2. Находим спектр ЭДС 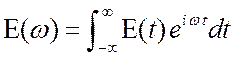 .
.
3. Находим спектр тока ![]() .
.
4. Находим сам ток, 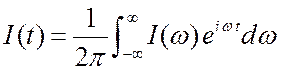 , выполняя обратное преобразование Фурье.
Никакого дифференциального уравнения составлять и решать на этом пути не надо.
, выполняя обратное преобразование Фурье.
Никакого дифференциального уравнения составлять и решать на этом пути не надо.
Таким образом,
комплексное сопротивление 2х-пол. полностью его характеризует. Зная ![]() , можно определить ток в цепи при
произвольном воздействии. Спектральный подход используется чаще при анализе
цепей. Многочисленные примеры мы рассмотрим позже, для четырёхполюсников.
, можно определить ток в цепи при
произвольном воздействии. Спектральный подход используется чаще при анализе
цепей. Многочисленные примеры мы рассмотрим позже, для четырёхполюсников.
Теперь мы рассмотрим примеры 2х-пол., которые очень часто встречаются в различных схемах.
3.4.2. Реальный индуктивный элемент.
Он изображён на рис.
3.7а. ![]() . Величину
. Величину ![]() называют
постоянной времени цепи (она имеет размерность времени). Безразмерная величина
называют
постоянной времени цепи (она имеет размерность времени). Безразмерная величина ![]() есть добротность индуктивного элемента на
частоте
есть добротность индуктивного элемента на
частоте ![]() (фактически
(фактически ![]() есть
угол). Обычно
есть
угол). Обычно ![]() .
. 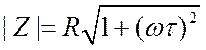 определяет
отношение амплитуд напряжения и тока, а аргумент
определяет
отношение амплитуд напряжения и тока, а аргумент ![]() даёт
сдвиг фаз между ними. В индуктивном элементе ток отстаёт от напряжения. На рис.
3.7 изображены зависимости сопротивления от частоты и векторные диаграммы. При
большой добротности угол
даёт
сдвиг фаз между ними. В индуктивном элементе ток отстаёт от напряжения. На рис.
3.7 изображены зависимости сопротивления от частоты и векторные диаграммы. При
большой добротности угол ![]() мал,
мал, ![]() . Его называют углом потерь.
. Его называют углом потерь.
3.4.3. Реальный ёмкостной элемент.
Он изображён на рис.
3.8а. Его проводимость ![]() . Сопротивление
. Сопротивление 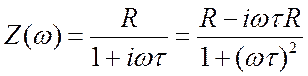 .
. 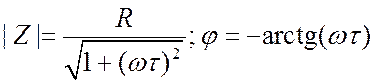 .
Постоянная времени
.
Постоянная времени ![]() (сек.), а добротность
(сек.), а добротность ![]() . Теперь ток опережает напряжение.
Соответствующие зависимости и векторные диаграммы изображены на рис.3.8.
. Теперь ток опережает напряжение.
Соответствующие зависимости и векторные диаграммы изображены на рис.3.8. ![]() есть угол потерь.
есть угол потерь.
3.4.4. Последовательный колебательный контур.
Оба реактивных элемента и
сопротивление теперь включены последовательно, рис. 3.9а. Выпишем сразу разные
выражения для сопротивления и приведём стандартные обозначения и термины. ![]()
![]() .
(3.6) Здесь:
.
(3.6) Здесь: ![]() - резонансная частота;
- резонансная частота; ![]() - характеристическое сопротивление;
- характеристическое сопротивление; ![]() - добротность;
- добротность; ![]() -
безразмерная частота;
-
безразмерная частота; ![]() - обобщённая расстройка.
Разность
- обобщённая расстройка.
Разность ![]() есть абсолютная расстройка, а
есть абсолютная расстройка, а ![]() - относительная. Если
- относительная. Если ![]() , то говорят, что расстройка мала. При этом
, то говорят, что расстройка мала. При этом
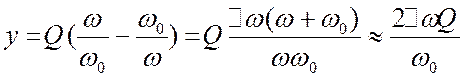 . Часто
. Часто ![]() .
.
В первую очередь, нас
интересует поведение сопротивления ![]() вблизи резонансной
частоты
вблизи резонансной
частоты ![]() , при малых расстройках. Эти зависимости
приведены на рис. 3.9. На резонансной частоте сопротивление последовательного
контура активно и минимально (
, при малых расстройках. Эти зависимости
приведены на рис. 3.9. На резонансной частоте сопротивление последовательного
контура активно и минимально (![]() ), а ток
), а ток ![]() - максимален. При этом напряжение на реактивных
элементах контура в
- максимален. При этом напряжение на реактивных
элементах контура в ![]() раз больше, чем на контуре в целом.
Поэтому говорят о резонансе напряжений. Типичные векторные диаграммы для трёх
частот приведены на рис. 3.10. Там же приведена зависимость тока в контуре от
частоты. Ток уменьшается в
раз больше, чем на контуре в целом.
Поэтому говорят о резонансе напряжений. Типичные векторные диаграммы для трёх
частот приведены на рис. 3.10. Там же приведена зависимость тока в контуре от
частоты. Ток уменьшается в ![]() раз при расстройке
раз при расстройке ![]() , когда
, когда ![]() . При
этом
. При
этом ![]() . Величину
. Величину ![]() называют
полосой пропускания. Если
называют
полосой пропускания. Если ![]() , то
, то ![]() .
.
3.4.5. Параллельный контур с идеальным конденсатором.
Схема контура изображена
на рис. 3.11а. ![]() . Остальные обозначения в
формулах такие же, как в пункте 3.4.4.
. Остальные обозначения в
формулах такие же, как в пункте 3.4.4. 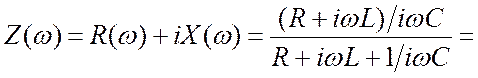
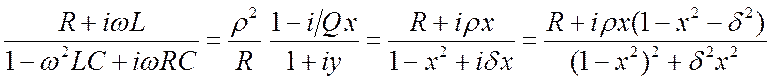 .
(3.7)
.
(3.7)
Характерные зависимости от частоты приведены на рис. 3.11. Резонансная частота
теперь не равна ![]() . Она определяется из равенства
. Она определяется из равенства ![]() , т.е.
, т.е. 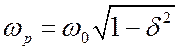 .
Однако, если
.
Однако, если ![]() , то отличие ничтожное. На резонансной
частоте сопротивление параллельного контура активно и максимально. Оно равно
, то отличие ничтожное. На резонансной
частоте сопротивление параллельного контура активно и максимально. Оно равно ![]() (При
(При ![]() ).
(3.8)
).
(3.8)
При этом ток в контуре большой (![]() ), а в общей цепи в
), а в общей цепи в ![]() раз меньше (
раз меньше (![]() ).
Поэтому иногда говорят о резонансе токов. Чаще используется другая
терминология. Резонанс в последовательном контуре называют последовательным
резонансом (сопротивление минимально), а в параллельном контуре – параллельным
(сопротивление максимально).
).
Поэтому иногда говорят о резонансе токов. Чаще используется другая
терминология. Резонанс в последовательном контуре называют последовательным
резонансом (сопротивление минимально), а в параллельном контуре – параллельным
(сопротивление максимально).
Попробуйте самостоятельно нарисовать векторные диаграммы напряжений и токов для параллельного контура на разных частотах.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.