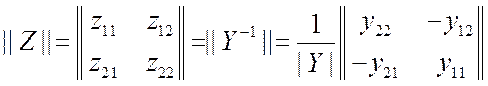Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 7

.

Элементы всех матриц однозначно связаны друг с другом. В качестве примера перейдём от матрицы  к матрице . Последняя широко используется в общей теории 4 ^х-пол. и на практике. Исходная система уравнений (3.16), хотим получить такую: 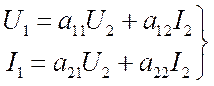.                                                         (3.17) Выразив  из второго уравнения исходной системы, 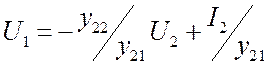, мы получим первое уравнение искомой. Сравнивая их, имеем:  . Теперь осталось исключить  из первого уравнения исходной системы, и мы придём ко второму уравнению искомой. Тогда: 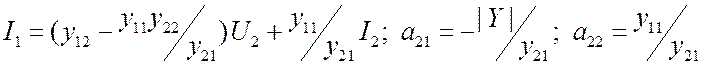.  есть определитель матрицы . Обратный переход даёт: . Все элементы матрицы  имеют одинаковую размерность. Элементы матрицы  имеют разную размерность;  и  безразмерны,  имеет размерность сопротивления,  - проводимости.

Аналогично можно связать элементы других матриц. Сделайте это самостоятельно, в качестве упражнения. Результат приведён в таблице 3.1 для четырёх систем, которые чаще используются.

Таблица 3.1.

Приведём ещё выражения для определителей систем.

.

3.6.2.  Число независимых элементов матриц.

В общем случае необратимого линейного 4 ^х-пол. все четыре комплексных элемента матриц независимы. Для обратимого (пассивного) 4 ^х-пол. только три элемента матриц являются независимыми, поскольку обратимость даёт равенство миноров исходной системы контурных токов (), что, в свою очередь, приводит к равенствам: .           (3.18)

По этой причине, для пассивных 4 ^х-пол. широко используются две эквивалентные схемы замещения, изображённые на рис. 3.18, Т – образная и П – образная. Они содержат по три комплексных сопротивления, что и позволяет реализовать эквивалентность. Полностью эквивалентными будут два 4 ^х-пол., имеющие одинаковые матрицы.

Если обратимый 4 ^х-пол. ещё и симметричен, то только два элемента матриц будут независимыми. Покажем это. Для симметричного 4 ^х-пол. мы можем поменять местами вход и выход, и при этом ничего не должно измениться. Пусть система уравнений с матрицей  характеризует 4 ^х-пол. для прямого направления передачи, рис. 3.19а. Напишем систему для обратного направления передачи, от выхода ко входу, сохранив сначала направления токов. Матрица системы будет обратная, . . Изменим теперь направление токов, как на рис. 3.19б, чтобы получить стандартное для обратного направления передачи. . Тогда получим систему с матрицей .. Для симметричного 4 ^х-пол. матрицы  и  должны быть одинаковы. В итоге, для обратимого () симметричного 4 ^х-пол. приходим к равенству . Это условие для других матриц приводит к следующим равенствам: .                                                           (3.19)

Для эквивалентных Т – образных и П – образных схем замещения, симметрия требует равенства сопротивлений, . Остаётся два независимых элемента.

3.6.3.  Использование различных систем уравнений.

Пока мы имеем дело с одним 4 ^х-пол., все системы уравнений равноправны. Всё определяется тем, какие переменные нам заданы, какие надо определить. Матрица  является в некотором смысле базовой, поскольку она получается непосредственно из исходной системы уравнений контурных токов, и независимыми переменными выступают напряжения.

Дополнительные соображения по использованию конкретной системы появляются тогда, когда мы соединяем несколько 4 ^х-пол. Пусть их будет два. Различают пять способов их соединения.

Отвлечёмся немного и дадим определение регулярных соединений. Изложенная выше теория 4 ^х-пол. базируется на предположении равенства токов для обоих входных зажимов, ток , и, как следствие, равенства токов для выходных, ток . Соединения 4 ^х-пол., при которых это условие не нарушается для каждого 4 ^х-пол. в отдельности, и принято называть регулярными. Когда это условие нарушается, тогда изложенная простая теория уже не годится. Нужно использовать другую, более сложную. Это мы обсудим в следующем параграфе, а сейчас вернёмся к соединениям.