Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 4

3.4.6. Параллельный контур с идеальной индуктивностью.

Схема контура представлена на рис. 3.12. В данном случае удобнее начать с общей проводимости контура, которая равна сумме проводимостей ветвей. 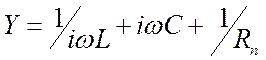. Сопротивление является обратной величиной. 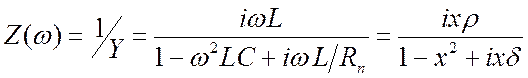;  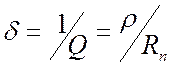.                     (3.9)

Для такого контура резонансная частота . Сравним выражения (3.7) и (3.9). Они отличаются малой добавкой  в числителе выражения (3.7). Если  велико и расстройка мала, то  и оба выражения практически совпадают. Условие их приближённой эквивалентности получится, если приравнять значения .  или .                                                             (3.10)

Оба параллельных контура имеют, практически, одинаковые характеристики. Таким образом, одну схему мы можем заменить другой, если она окажется удобнее в данной ситуации (пересчитав сопротивления). На практике, для уменьшения добротности контура, его часто шунтируют сопротивлением.

3.4.7.  Неполное (частичное) включение параллельного контура.

Реальная схема такого включения контура выглядит так, как на рис. 3.13а. Используется катушка индуктивности с отводом. Мы же для упрощения анализа не будем учитывать связь между частями катушки, а будем анализировать схему, приведённую на рис. 3.13б. Введём обозначения: ; . Тогда

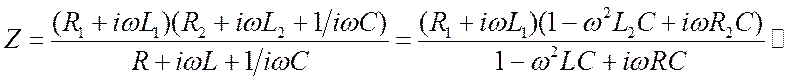
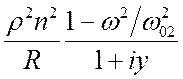. Последнее, более простое приближенное выражение (упрощён числитель) написано для большой добротности контура, когда  и , и удобно при анализе  вблизи частоты .

Анализ полного выражения показывает, что рассматриваемая цепь имеет две резонансные частоты. Параллельный резонанс имеет место на частоте  и определяется всеми элементами контура (знаменатель ). На частоте параллельного резонанса сопротивление контура  активно и максимально (). За счёт параметра  можно менять сопротивление  в широких пределах, осуществляя согласование сопротивлений. При этом резонансная частота и добротность практически не меняются. Именно это обстоятельство определяет широкое применение такой схемы включения контура.

Последовательный резонанс реализуется на частоте  только за счёт верхней ветви контура. На этой частоте сопротивление контура  активно и минимально. Качественное поведение активной  и реактивной  составляющих сопротивления контура изображено на рис. 3.13в.

Чем сложнее схема, тем более громоздкое и сложное получается выражение для . Анализ его затруднён. Однако при большой добротности элементов цепи качественный анализ поведения  значительно упрощается, если вообще пренебречь потерями. Для данного примера получим ().  Эта зависимость изображена пунктиром на рис. 3.13в. На частоте  получается разрыв.

3.4.8.  Общие свойства функции .

Приведённые примеры (и другие) позволяют сформулировать некоторые общие свойства функции  для любых пассивных двухполюсников. Импеданс . Здесь  и  есть активная и реактивная составляющие сопротивления на заданной частоте. Модуль  определяет отношение амплитуд напряжения и тока, а аргумент  - сдвиг фаз между ними.

1. . Пассивная цепь может только поглощать энергию. Равенство реализуется только для чисто реактивной цепи (без потерь). Как следствие, .

2. Функция  есть дробно – рациональная функция частоты  (точнее параметра ), т.е. отношение двух полиномов. При этом степени полиномов в числителе и знаменателе  не могут отличаться больше, чем на единицу.

3.  и  есть чётные функции частоты, а  и  - нечётные.

4. В сложной цепи последовательные и параллельные резонансы чередуются.

3.5. Четырёхполюсники.

Четырёхполюсник (4 ^х-пол.) представляет некоторую цепь, имеющую вход и выход. Обычно 4 ^х-пол. включается между генератором и нагрузкой, как изображено на рис. 3.14, где указаны стандартные направления токов и напряжений. Входные параметры имеют индекс «1», выходные – индекс «2». . При этом ток  одинаков для входных зажимов (клемм) 4 ^х-пол., ток  одинаков для выходных.

Различают четырёхполюсники: 1. Активные и пассивные. Активные содержат внутри генераторы (обычно зависимые).

2. Линейные и нелинейные. Линейные содержат только линейные элементы.