Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 18

Определяем коэффициент передачи .Здесь , . Выпишем сразу разные выражения для .  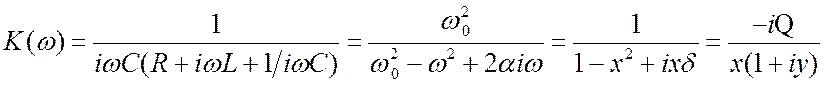  (3.52) .

Точно такой же коэффициент передачи имеет очень похожая цепь, последовательный колебательный контур с идеальной индуктивностью, рис. 3.59б. Для неё . Добротность двух вариантов этой цепи будет одинакова, если , или .

Характерные значения :  при любом значении ; , как , когда . При большой добротности контура, изображённые цепи являются узкополосными полосовыми фильтрами. При малой добротности они широко используются  как ФНЧ. Рассмотрим сначала такое их применение.

3.9.2.  Последовательный колебательный контур как ФНЧ.

Для анализа коэффициента передачи наиболее удобно такое выражение. 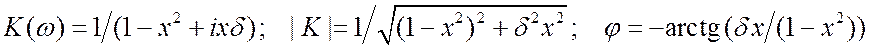.  (3.53)

Это тоже цепь второго порядка, только здесь  может принимать любые значения (практически  ), в отличие от  цепей, где было . При значениях  мы уже анализировали эти выражения и выяснили, что качество фильтра улучшается при уменьшении  (, если ; , если ). Эта тенденция сохраняется и для  фильтров НЧ. На рис. 3.60 представлены типичные характеристики таких фильтров. При этом, на рис. 3.60б изображены те же зависимости, но с другими масштабами по осям ради  удобства сравнения и бóльшей наглядности. По оси абсцисс отложено отношение , где  есть граничная частота (своя для каждого фильтра) на уровне 0,71 от максимума.

При дальнейшем уменьшении , характер поведения  меняется и на характеристике (при ), появляется максимум, «выброс», который становится всё больше, достигая уровня , при  . Если полосу пропускания фильтра определять на уровне  от максимального значения, то дальнейшее уменьшение  уже невозможно (мы получим полосовой фильтр). Таким образом, определился интервал типичных значений  для  фильтров НЧ ().

Значение  приводит нас к фильтру Баттерворса второго порядка, для которого 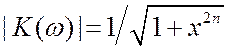, где  - порядок фильтра. Приведённая функция Баттерворса даёт максимально «плоскую» характеристику при , без выброса (все производные до порядка  равны нулю при ). При этом, . Когда , выброс составляет уже 15% (при ), но зато спад характеристики вблизи граничной частоты происходит ещё быстрее,  (). Наконец, при , . Бóльшего значения с помощью  фильтров второго порядка уже не получить (фильтр Баттерворса третьего порядка даёт ).

Фазовая характеристика, рис. 3.61, ведёт себя  сначала, как для  фильтров, но потом, по мере уменьшения , она тоже меняет характер своего поведения. На ней появляется точка перегиба. Когда , она реализуется при , и фазовая характеристика ФНЧ получается наиболее линейна на начальном участке (постоянная задержка). При уменьшении  точка перегиба перемещается направо к значению .

Фильтр ВЧ можно реализовать, если снимать напряжение с индуктивного элемента, как на рис. 3. 59в. При этом . Это выражение можно получить из выражения (3.53), путём частотной трансформации. Надо заменить . Тогда характеристики легко получаются из приведённых на рис. 3.60 и 3.61. Зависимость  выглядит так же, если считать, что по оси абсцисс отложена величина . Фазовую характеристику ФНЧ надо просто сместить на  вверх.

3.9.3. Переходная характеристика  фильтра НЧ.

В этом примере и в следующих будем использовать преобразование Лапласа. Пусть значения  и . Тогда , . 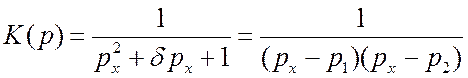, где  есть корни характеристического уравнения . При , корни были вещественные. Теперь они образуют комплексно - сопряжённую пару , 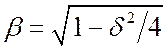. Это и определяет особенность поведения . Пусть . Тогда: ; . .

 В итоге,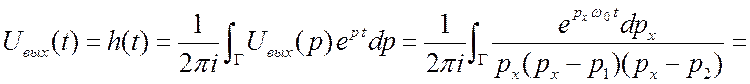

.   (3.54) Здесь 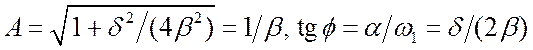. Следует отметить, что при , корень характеристического уравнения получается кратным () и . Получите этот результат самостоятельно. Переходные характеристики при разных значениях  приведены на рис. 3.62. На переходной характеристике теперь тоже появляется «выброс», но зато нарастание напряжения на выходе происходит быстрее. Пока «выброс» небольшой, это не страшно. При наличии «выброса», длительность фронта сигнала становится меньше. Напомним, что длительность фронта есть время нарастания сигнала от уровня 0,1 до уровня 0,9 установившегося значения (равного единице).  Оценки дают следующие значения длительности фронта: ,  (для  фильтров при  ). Разница очень существенная. Качественные фильтры НЧ всегда имеют некоторый «выброс» на переходной характеристике, даже если нет «выброса» на частотной.