Общая схема такой цепи уже была изображена на рис.
3.27. Там же была приведена и матрица ![]() для
этой цепи. Найдём сначала коэффициент передачи в общем виде, для произвольных
сопротивлений, а потом рассмотрим конкретные примеры. Для простоты, как и
раньше, предположим, что внешняя нагрузка уже учтена и включена в
для
этой цепи. Найдём сначала коэффициент передачи в общем виде, для произвольных
сопротивлений, а потом рассмотрим конкретные примеры. Для простоты, как и
раньше, предположим, что внешняя нагрузка уже учтена и включена в ![]() , а
, а ![]() . Тогда,
полагая
. Тогда,
полагая ![]() , из общей формулы (3.22) получим
, из общей формулы (3.22) получим ![]() . Нам нужен только один элемент матрицы
. Нам нужен только один элемент матрицы ![]() этой цепи (выражение (3.27)).
этой цепи (выражение (3.27)). ![]() . В итоге:
. В итоге:![]() .
(3.42)
.
(3.42)
Изображённая цепь позволяет реализовать ![]() фильтры второго порядка НЧ, ВЧ и
полосовые. Начнём с ФНЧ.
фильтры второго порядка НЧ, ВЧ и
полосовые. Начнём с ФНЧ.
3.8.5.1. Двухзвенный фильтр НЧ.
Схема такого фильтра представлена на рис. 3.44а. В
данном примере: ![]() . Примем обозначения:
. Примем обозначения: ![]()
![]() . Введём также удобные
параметры:
. Введём также удобные
параметры: ![]() есть характерная частота (
есть характерная частота (![]() );
); ![]() -
безразмерная (относительная) частота (
-
безразмерная (относительная) частота (![]() получается
порядка единицы в интересующей нас области частот);
получается
порядка единицы в интересующей нас области частот); ![]() -
«затухание» (по аналогии с колебательным контуром). Можно показать, что для
-
«затухание» (по аналогии с колебательным контуром). Можно показать, что для ![]() цепей
цепей ![]() . Тогда
. Тогда
 . (3.43) Последнее выражение, в которое
входят только безразмерные параметры, получилось очень простое.
. (3.43) Последнее выражение, в которое
входят только безразмерные параметры, получилось очень простое. 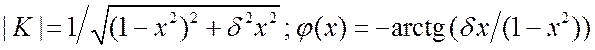 . Максимальное значение
. Максимальное значение ![]() реализуется при
реализуется при ![]() .
Полоса пропускания фильтра, определённая на уровне
.
Полоса пропускания фильтра, определённая на уровне ![]() ,
находится из уравнения
,
находится из уравнения ![]() . Отсюда
. Отсюда 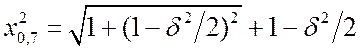 .
.
На практике часто используют два одинаковых звена. При
этом: ![]()
![]() .
Характеристики для этого случая изображены на рис. 3.44. Двухзвенный ФНЧ
оказался лучше, чем однозвенный, но не сильно. Такой путь улучшения качества не
перспективен. Как мы увидим дальше, значительное улучшение качества получится,
если сопротивления заменить индуктивностями, т.е. перейти к
.
Характеристики для этого случая изображены на рис. 3.44. Двухзвенный ФНЧ
оказался лучше, чем однозвенный, но не сильно. Такой путь улучшения качества не
перспективен. Как мы увидим дальше, значительное улучшение качества получится,
если сопротивления заменить индуктивностями, т.е. перейти к ![]() фильтрам.
фильтрам.
Качество ![]() фильтров улучшается по
мере уменьшения параметра
фильтров улучшается по
мере уменьшения параметра ![]() . Такова общая
тенденция. Минимальное значение
. Такова общая
тенденция. Минимальное значение ![]() в рамках указанной
схемы можно реализовать только в том случае, если устранить влияние второго
звена на первое. Для этого между ними включают некоторое «буферное» устройство
(рис. 3.44а) с большим входным сопротивлением и малым выходным (например,
эмиттерный повторитель). Тогда подключение второго звена не меняет коэффициент
передачи первого. При этом можно перемножать коэффициенты передачи отдельных
звеньев. Для двух одинаковых звеньев будем иметь:
в рамках указанной
схемы можно реализовать только в том случае, если устранить влияние второго
звена на первое. Для этого между ними включают некоторое «буферное» устройство
(рис. 3.44а) с большим входным сопротивлением и малым выходным (например,
эмиттерный повторитель). Тогда подключение второго звена не меняет коэффициент
передачи первого. При этом можно перемножать коэффициенты передачи отдельных
звеньев. Для двух одинаковых звеньев будем иметь: ![]() .
Характеристики для этого случая тоже представлены на рис. 3.44.
.
Характеристики для этого случая тоже представлены на рис. 3.44.
Переходные характеристики мы рассмотрим немного позже сразу для всех фильтров второго порядка.
3.8.5.2. Двухзвенный фильтр ВЧ.
В схеме фильтра НЧ, рис. 3.44а, поменяем местами
сопротивления и конденсаторы. Получим ФВЧ, рис. 3.45а. Это опять
идеализированная цепь. Теперь: ![]() . Постоянные времени и
другие параметры вводятся так же, как и для ФНЧ. В итоге:
. Постоянные времени и
другие параметры вводятся так же, как и для ФНЧ. В итоге: ![]() . (3.44)
. (3.44) 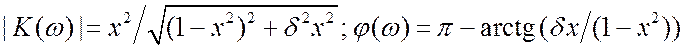 . На
рис. 3.45б приведена типичная зависимость
. На
рис. 3.45б приведена типичная зависимость ![]() от
частоты для одинаковых звеньев.
от
частоты для одинаковых звеньев. ![]() ;
; ![]() .
. ![]() , когда
, когда ![]() . Степень полиномов в числителе и знаменателе
. Степень полиномов в числителе и знаменателе
![]() одинакова (результат идеализации). Фазовая
характеристика ФВЧ получается путём сдвига фазовой характеристики ФНЧ, рис.
3.44в, на
одинакова (результат идеализации). Фазовая
характеристика ФВЧ получается путём сдвига фазовой характеристики ФНЧ, рис.
3.44в, на ![]() вверх.
вверх.
Коэффициент прямоугольности для ФВЧ надо вводить иначе.
Старое определение не годится, поскольку полоса пропускания бесконечна. Можно
определить ![]() . Для рассмотренного примера получим 0,14 (
. Для рассмотренного примера получим 0,14 (![]() ).
).
Отметим интересное обстоятельство. Приведённое
выражение (3.44) можно получить из аналогичного для ФНЧ, выражение (3.43),
заменив ![]() на
на ![]() . Эту
операцию называют частотной трансформацией.
. Эту
операцию называют частотной трансформацией.
3.8.5.3. Полосовые ![]() фильтры второго порядка.
фильтры второго порядка.
Такие фильтры получаются, если сделать комбинацию из
дифференцирующей и интегрирующей цепочек. Получим два варианта ПФ, изображённые
на рис. 3.46. ![]() есть постоянная времени
дифференцирующей цепи, а
есть постоянная времени
дифференцирующей цепи, а ![]() - постоянная времени
интегрирующей цепи.
- постоянная времени
интегрирующей цепи. ![]() . Коэффициент передачи будет
иметь одинаковый вид для обоих вариантов.
. Коэффициент передачи будет
иметь одинаковый вид для обоих вариантов.
![]() .
(3.45) Как и раньше,
.
(3.45) Как и раньше, ![]() .
. ![]() . Незначительные различия есть только в
параметре
. Незначительные различия есть только в
параметре ![]() .
. ![]() для
первого варианта цепи, и
для
первого варианта цепи, и ![]() для второго.
По-прежнему
для второго.
По-прежнему ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.