Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 12

Рассмотрим теперь искажение линейно нарастающего напряжения. Пусть . Воспользуемся формулой Дюамеля (3.14). . . 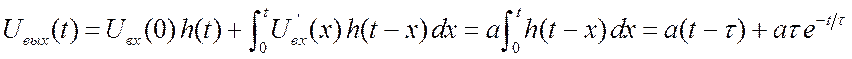 Этот результат изображён на рис. 3.36. Когда  , . Опять имеем интегрирование. Когда . Входной сигнал оказывается как бы задержанным на время .

Таким образом, , это и есть та временная область, где интегрирующая цепочка осуществляет интегрирование входного сигнала, независимо от его формы. Чем больше постоянная времени цепи , тем шире временная область, тем качественнее интегрирование.

В заключение рассмотрим искажение прямоугольного импульса длительности . Пусть . Тогда выходное напряжение получится путём вычитания двух переходных характеристик,  и .На рис. 3.37 приведены качественные результаты для трёх соотношений  и . Малые искажения формы сигнала будут в последнем случае, когда .

Интегрирующая цепочка «сглаживает» особенности входного сигнала. Например, если на входе сигнал меняется скачком, то на выходе мы будем иметь непрерывный сигнал.

3.8.2. Активный делитель с ёмкостью.

Многие простые цепи имеют вид делителя из двух сопротивлений, рис. 3.38. Надо просто запомнить его коэффициент передачи и пользоваться им. . Для данного примера, рис. 3.39а: , где ; . Здесь: ; . Всё свелось к интегрирующей цепи.

Рассмотренная цепь представляет схему реального делителя. Даже если мы не ставим явно конденсатор на выход цепи, он всё равно там образуется за счёт входной ёмкости нагрузки, ёмкости проводов, монтажа. В результате получается интегрирующая цепь, т.е. ФНЧ.

3.8.3.  Компенсированный делитель.

Он изображён на рис. 3.39б. Добавили конденсатор . Теперь: ;

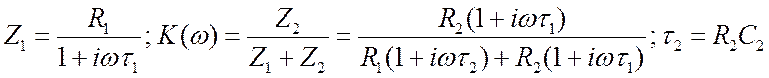. Если , то  и не зависит от частоты. Конденсатор  компенсирует влияние конденсатора . Такие широкополосные делители очень часто используются во многих приборах и устройствах.

Рассмотрим пример. Пусть сопротивление  мом и ёмкость  пф образуют входной импеданс осциллографа (вместе с кабелем). Сделаем делитель в 10 раз на входе кабеля. Тогда надо взять  мом и  пф. Получили компенсированный делитель, входной импеданс которого образуется сопротивлением 10 мом и ёмкостью 10 пф.

3.8.4. Дифференцирующая цепь. Элементарный ФВЧ.

Варианты цепи изображены на рис. 3.40. Нужно сразу отметить идеализированный характер этих цепей, их нереальность. Например, в реальной  цепи параллельно с сопротивлением окажется некоторая ёмкость монтажа и нагрузки, а на входе – сопротивление генератора. Влияние этих элементов неизбежно проявится, но на более высоких частотах, по сравнению с рассматриваемыми.

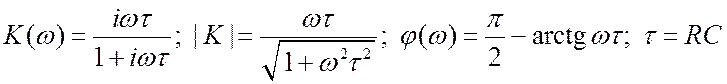.                 (3.41)

Для  цепи . Зависимость от частоты изображена на рис. 3.40в. Зависимость  получится, если аналогичную зависимость для интегрирующей цепочки (рис.3.34в) поднять на  вверх. Сдвиг фазы будет меняться от  до 0.

Если , то  даёт оператор дифференцирования. Поэтому цепочку и называют дифференцирующей. Идеализированная цепочка представляет элементарный ФВЧ, но тоже плохой. Реальная цепочка представляет уже полосовой фильтр.

Перейдём к анализу переходной характеристики , рис. 3.41. Скачок напряжения на входе (и другие особенности входного напряжения, изломы, скачки производных) дифференцирующая цепочка воспроизводит полностью. В какой временной области мы получим дифференцирование входного сигнала? В области , когда . Для улучшения качества дифференцирования надо уменьшать .

Пусть теперь  растёт по линейному закону. Тогда выходное напряжение 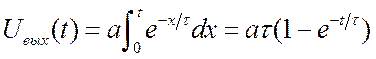 приведено на рис. 3.42. Когда , . Излом входного напряжения при  цепочка воспроизводит полностью. Когда , . Это область дифференцирования.

На рис. 3.43 изображены типичные искажения прямоугольного импульса при различных соотношениях постоянной времени цепочки  и длительности импульса . Малые искажения импульса получаются при условии .

Рассмотренные простейшие  цепи относят к цепям первого порядка, поскольку в знаменателе  стоит полином первого порядка. Перейдём теперь к более сложным цепям второго порядка.

3.8.5. Двухзвенные цепи.