1. Цепное или каскадное
соединение. При таком соединении вход второго
4 х-пол. подключается к выходу первого, рис. 3.20. Такое соединение
4 х-пол. будет всегда регулярным. Эти два 4 х-пол. мы
можем заменить одним. Как найти элементы общей матрицы ![]() ,
зная матрицы
,
зная матрицы ![]() и
и ![]() ?
Исходные уравнения:
?
Исходные уравнения: 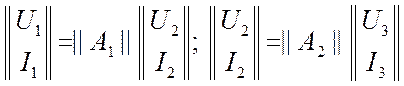 . Подставляя второе равенство в
первое, получим результат.
. Подставляя второе равенство в
первое, получим результат. 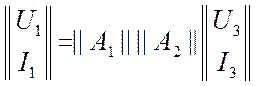 . Ответ:
. Ответ: ![]() .
.
При каскадном соединении
4 х-пол. матрицы ![]() перемножаются. Такое соединение
4 х-пол. встречается чаще всего, что и объясняет широкое использование
матрицы
перемножаются. Такое соединение
4 х-пол. встречается чаще всего, что и объясняет широкое использование
матрицы ![]() .
.
2. Параллельно –
параллельное соединение (или просто параллельное). Необходимость двойной
терминологии возникает потому, что надо указывать как соединены входы и выходы
4 х-пол. При таком соединении общими (одинаковыми) переменными для
обоих 4 х-пол. являются напряжения, рис. 3.21, поэтому удобнее всего
использовать систему уравнений с матрицей ![]() . Токи в
узлах суммируются.
. Токи в
узлах суммируются. ![]() . Эти два 4 х-пол.
тоже можно заменить одним. Если регулярность соединения не нарушается, то общая
матрица
. Эти два 4 х-пол.
тоже можно заменить одним. Если регулярность соединения не нарушается, то общая
матрица ![]() . Для доказательства надо сложить левые и
правые части систем уравнений.
. Для доказательства надо сложить левые и
правые части систем уравнений. 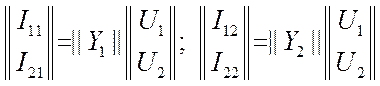 . Получим
. Получим 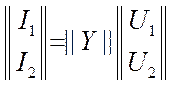 .
.
В общем случае такого соединения
4 х-пол. регулярность соединения нарушается. Отметим, не
останавливаясь на доказательстве, три важных случая такого соединения, для
которых регулярность имеет место. 1. Соединение уравновешенных 4 х-пол.
2. Соединение «треугольных» 4 х-пол. (фактически трехполюсников).
«Треугольными» называют такие 4 х-пол., у которых один входной зажим
и один выходной закорочены. При этом закороченные зажимы одного должны
соединяться с закороченными зажимами другого, как на рис. 3.21б.
3. Соединения подобных 4 х-пол. У подобных 4 х-пол. схемы
одинаковы, а величины элементов пропорциональны.
3. Последовательно –
последовательное соединение (или просто последовательное), рис. 3.22. При таком
соединении 4 х-пол. общими (одинаковыми) переменными являются токи
(при условии регулярности). Напряжения на входе и выходе суммируются. Легко
убедиться в том, что в данном случае при переходе к общей матрице, складываться
будут элементы матриц сопротивлений. ![]() . К сожалению,
регулярность имеет место только при соединении «треугольных» 4 х-пол.,
как указано на рис. 3.22б.
. К сожалению,
регулярность имеет место только при соединении «треугольных» 4 х-пол.,
как указано на рис. 3.22б.
4. Смешанные соединения,
последовательно – параллельное, рис 3.23, и параллельно – последовательное. В
этом случае будут складываться элементы матриц ![]() или
или ![]() соответственно.
соответственно.
3.6.4. Общая матрица.
Она используется тогда,
когда токи входных зажимов (а следовательно и выходных) разные. Рассмотрим эту
ситуацию очень коротко. Буквы «в» и «н» означают верхние и нижние зажимы.
Ситуация и обозначения отражены на рис. 3.24. Вводят 8 переменных, 4
напряжения и 4 тока. Они связаны двумя очевидными соотношениями. ![]() . Остаётся 6 переменных. Определяют 3
напряжения и 3 тока следующим образом.
. Остаётся 6 переменных. Определяют 3
напряжения и 3 тока следующим образом. ![]() и
и ![]() есть входное и выходное напряжения, как и
раньше.
есть входное и выходное напряжения, как и
раньше. ![]() есть разность потенциалов между точками C и D
на рис. 3.24. Потенциалы этих точек равны соответственно полусумме потенциалов
входных и выходных зажимов.
есть разность потенциалов между точками C и D
на рис. 3.24. Потенциалы этих точек равны соответственно полусумме потенциалов
входных и выходных зажимов.
![]() .
.
![]() .
.
Из общей системы
уравнений контурных токов мы можем путём преобразований получить линейную
систему из трёх уравнений, связывающих 6 введённых переменных. Пусть это будет
система с матрицей проводимостей ![]() .
. ![]() , где
, где ![]() и
и ![]() есть векторы тока и напряжения, т.е.
матрицы, имеющие один столбец. Однако теперь матрица
есть векторы тока и напряжения, т.е.
матрицы, имеющие один столбец. Однако теперь матрица ![]() содержит
не 4, а 9 элементов. Такая система используется в общем случае, при нарушении
регулярности соединений 4 х-пол. (если
содержит
не 4, а 9 элементов. Такая система используется в общем случае, при нарушении
регулярности соединений 4 х-пол. (если ![]() ).
).
Ток ![]() введён так, что он обращается в ноль, если
введён так, что он обращается в ноль, если
![]() . Тогда последнее уравнение становится
лишним. С его помощью
. Тогда последнее уравнение становится
лишним. С его помощью ![]() выражается через
выражается через ![]() и
и ![]() , и
исключается из системы. Мы переходим к рассмотренной ранее системе с матрицей
, и
исключается из системы. Мы переходим к рассмотренной ранее системе с матрицей ![]() , что значительно проще.
, что значительно проще.
3.6.5. Общие формулы для параметров четырёхполюсника.
Получим теперь общие
формулы для входного и выходного сопротивлений, коэффициентов передачи 4 х-пол.
через элементы матриц. Ситуация изображена на рис. 3.14. За основу возьмём
матрицу ![]() и соответствующую систему уравнений
(3.17).
и соответствующую систему уравнений
(3.17). ![]() .
. ![]() .
Однако здесь мы приведём сводку формул и для других элементов матриц..
.
Однако здесь мы приведём сводку формул и для других элементов матриц..
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.