В областях с нормальной дисперсией ![]() . Только в окрестности минимума
. Только в окрестности минимума ![]() существуют области с аномальной
дисперсией. На частотах (конечных), где
существуют области с аномальной
дисперсией. На частотах (конечных), где ![]() ,
возможен скачок фазы на
,
возможен скачок фазы на ![]() вверх.
вверх.
На комплексной плоскости частоты ![]() , или
, или ![]() ,
функция
,
функция ![]() имеет только полюса и нули. Других особых
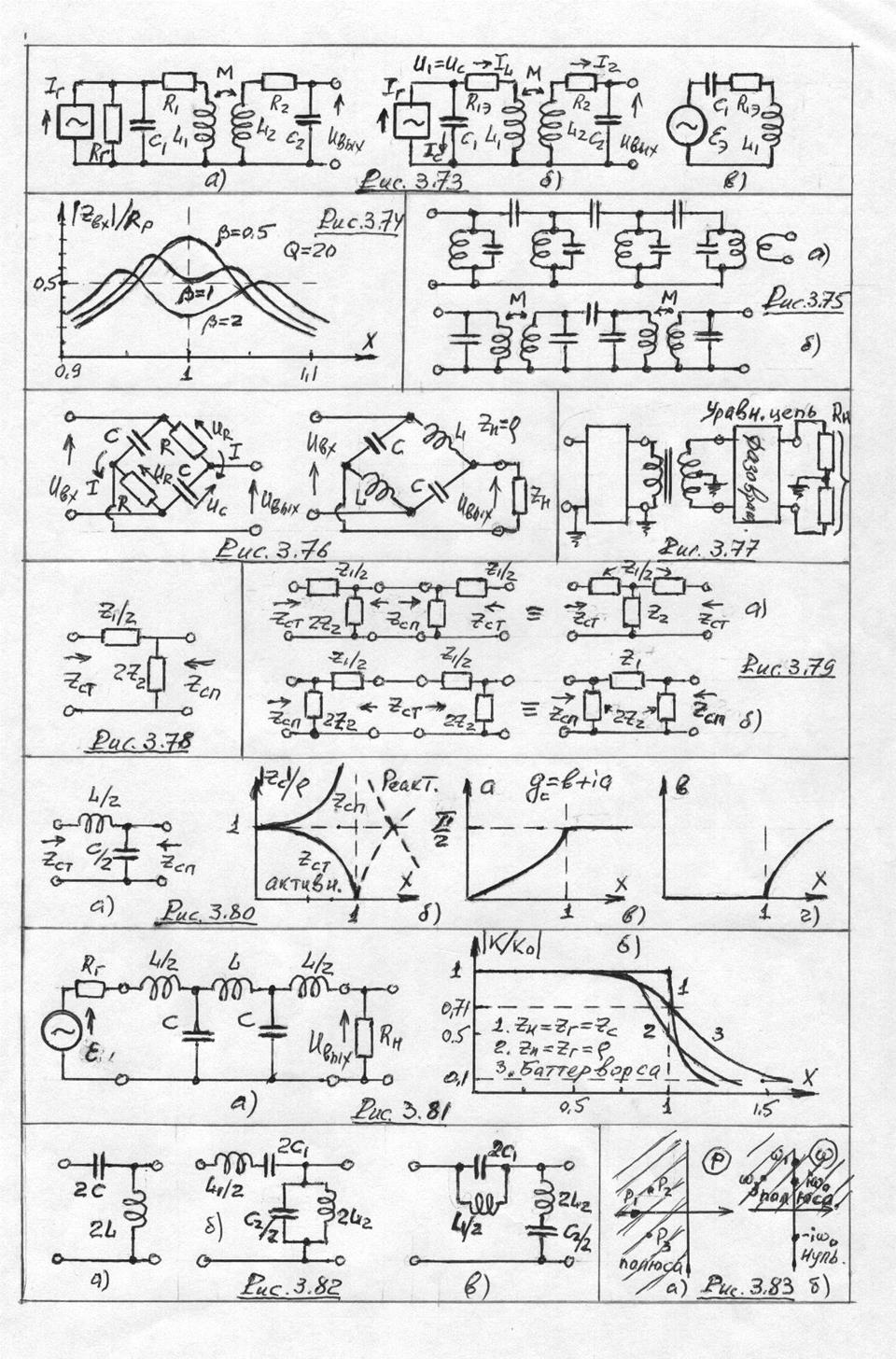
точек нет. При этом полюса могут находиться только в заштрихованных на рис.
3.83 полуплоскостях. Таким полюсам соответствуют устойчивые (затухающие со
временем) процессы. Если потери не учитываются, то полюса могут оказаться на
границе областей (идеализация, чисто реактивные цепи). Каждому простому полюсу
имеет только полюса и нули. Других особых
точек нет. При этом полюса могут находиться только в заштрихованных на рис.
3.83 полуплоскостях. Таким полюсам соответствуют устойчивые (затухающие со
временем) процессы. Если потери не учитываются, то полюса могут оказаться на
границе областей (идеализация, чисто реактивные цепи). Каждому простому полюсу ![]() , или
, или ![]() , в
переходном процессе соответствует вычет
, в
переходном процессе соответствует вычет ![]() .
Каждой паре комплексно сопряженных полюсов
.
Каждой паре комплексно сопряженных полюсов ![]() на
плоскости
на
плоскости ![]() , соответствует решение
, соответствует решение ![]() . В любом случае эти решения убывают с
ростом времени и дают устойчивые процессы. Поэтому реакция цепи на любое
кратковременное воздействие (типа короткого импульса,
. В любом случае эти решения убывают с
ростом времени и дают устойчивые процессы. Поэтому реакция цепи на любое
кратковременное воздействие (типа короткого импульса, ![]() ),
в частности импульсная характеристика
),
в частности импульсная характеристика ![]() , должна
исчезать по мере увеличения t. Пишут,
, должна
исчезать по мере увеличения t. Пишут, ![]() , когда
, когда ![]() . Реакция цепи на ступенчатое воздействие,
переходная характеристика
. Реакция цепи на ступенчатое воздействие,
переходная характеристика ![]() , может и не исчезать,
но должна быть ограничена. Таким требованиям должны удовлетворять временные
характеристики реальных цепей.
, может и не исчезать,
но должна быть ограничена. Таким требованиям должны удовлетворять временные
характеристики реальных цепей.
Нули коэффициента передачи значительной части реальных цепей тоже находятся в заштрихованных полуплоскостях на рис. 3.83. Такие цепи называют минимально фазовыми. Для них реальная и мнимая части коэффициента передачи связаны преобразованиями Гильберта.
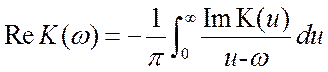 ;
; 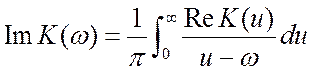 . Таким образом, для минимально фазовых
цепей имеет место взаимно однозначная связь между реальной и мнимой частями
коэффициента передачи. Зная одну часть, можно найти другую. Их нельзя задавать
независимо.
. Таким образом, для минимально фазовых
цепей имеет место взаимно однозначная связь между реальной и мнимой частями
коэффициента передачи. Зная одну часть, можно найти другую. Их нельзя задавать
независимо.
Аналогичные соотношения имеют место и для комплексной
функции ![]() .
. 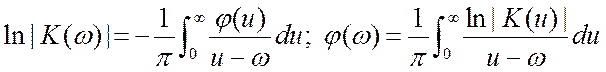 .
Амплитудно-частотная и фазо-частотная характеристики минимально фазовых цепей
однозначно связаны.
.
Амплитудно-частотная и фазо-частотная характеристики минимально фазовых цепей
однозначно связаны.
К неминимально фазовым цепям относятся, например,
фазовращатели, для которых ![]() . Нуль коэффициента
передачи находится в нижней полуплоскости, а полюс – в верхней, как указано на
рис. 3.83б. Для таких цепей нет взаимно однозначной связи между реальной и
мнимой частями коэффициента передачи. Их можно задавать независимо. Поэтому эти
цепи широко используются на практике для коррекции только фазовых характеристик.
. Нуль коэффициента
передачи находится в нижней полуплоскости, а полюс – в верхней, как указано на
рис. 3.83б. Для таких цепей нет взаимно однозначной связи между реальной и
мнимой частями коэффициента передачи. Их можно задавать независимо. Поэтому эти
цепи широко используются на практике для коррекции только фазовых характеристик.
При решении задач синтеза цепей по заданным
характеристикам, нужно учесть всё сказанное в этом параграфе относительно
особенностей характеристик. Всё это, разумеется, учтено в разработанном
аппарате синтеза цепей. Однако учесть это практически совсем не просто.
Например, мы хотим сделать ФНЧ и задали его характеристику (по неопытности)
такой, как для идеального фильтра. ![]() , когда
, когда ![]() , и
, и ![]() ,
когда
,
когда ![]() . Сдвиг фаз нас не интересует. Мы задали
некоторую вещественную функцию
. Сдвиг фаз нас не интересует. Мы задали
некоторую вещественную функцию ![]() и хотим знать, можно ли
сделать такой фильтр или нет? Ответ отрицательный. Это классический пример и
здесь всё просто. Для решения вопроса, надо найти импульсную характеристику
такого фильтра.
и хотим знать, можно ли
сделать такой фильтр или нет? Ответ отрицательный. Это классический пример и
здесь всё просто. Для решения вопроса, надо найти импульсную характеристику
такого фильтра. ![]() . Пусть
. Пусть ![]() .
Тогда
.
Тогда 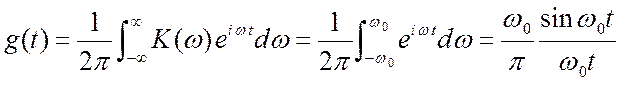 . Вроде бы всё нормально, интеграл
вычислили, однако результат абсурдный. Сигнал на выходе существует при
. Вроде бы всё нормально, интеграл
вычислили, однако результат абсурдный. Сигнал на выходе существует при ![]() , когда на входе ещё ничего не было. Делаем
разумный вывод, что фильтр с такой характеристикой неосуществим. Здесь
оказалось всё легко проверить. Как быть в других подобных случаях?
, когда на входе ещё ничего не было. Делаем
разумный вывод, что фильтр с такой характеристикой неосуществим. Здесь
оказалось всё легко проверить. Как быть в других подобных случаях?
Существуют критерии физической осуществимости,
которыми можно воспользоваться. Одним из таких критериев является широко
известный критерий Пейли – Винера. Если интеграл 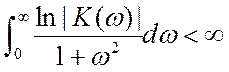 ,
сходится, то цепь с таким
,
сходится, то цепь с таким ![]() физически осуществима.
Для рассмотренного примера идеального ФНЧ интеграл расходится. Всё ясно. Однако
не надо «абсолютизировать» такие критерии. Даже если интеграл сойдётся, то
далеко не всегда такой
физически осуществима.
Для рассмотренного примера идеального ФНЧ интеграл расходится. Всё ясно. Однако
не надо «абсолютизировать» такие критерии. Даже если интеграл сойдётся, то
далеко не всегда такой ![]() можно реализовать на практике.
Требования должны быть очень разумны. Огромное значение тут играет опыт.
можно реализовать на практике.
Требования должны быть очень разумны. Огромное значение тут играет опыт.

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.