Мы познакомились с узкополосными полосовыми фильтрами хорошего качества. Теперь очень кратко обсудим вопрос о реализации других качественных фильтров (НЧ, ВЧ, широкополосных полосовых и режекторных). Такие фильтры тоже получаются с помощью реактивных элементов с большой добротностью. Только таким путём удаётся получить минимальное ослабление сигнала (минимальное затухание) в полосе пропускания. Использование активных сопротивлений внутри фильтров нежелательно, т.к. это только увеличивает ослабление, ухудшая качество фильтра. На начальном этапе, для упрощения анализа, вообще пренебрегают потерями, считая реактивные элементы идеальными. Примем это предположение.
В теории фильтров обычно подробно анализируются только ФНЧ. Другие фильтры рассматриваемого класса могут быть получены из ФНЧ путём соответствующего изменения схемы, а необходимые формулы, путём замены переменных. Это мы обсудим позже.
Итак, рассмотрим фильтры, содержащие только идеальные
реактивные элементы (без потерь). Элементарная ячейка таких фильтров,
полузвено, представляет просто делитель, рис. 3.78. В зависимости от характера
сопротивлений ![]() мы можем получить различные
фильтры. Вспомним матрицу A такого делителя и связь элементов этой матрицы с
характеристическими параметрами
мы можем получить различные
фильтры. Вспомним матрицу A такого делителя и связь элементов этой матрицы с
характеристическими параметрами ![]() (формулы 3.29 и 3.31).
(формулы 3.29 и 3.31).
![]() . Тогда:
. Тогда: ![]() ;
; ![]() . Путём каскадного соединения таких
полузвеньев, можно получить более сложные и качественные фильтры, например,
полные Т и П – образные звенья, рис. 3.79. Соединение полузвеньев
и звеньев производится по принципу идеального согласования внутри фильтра.
Характеристические сопротивления соединяемых частей должны быть одинаковы.
Поэтому такие фильтры иногда называют согласованными внутри.
. Путём каскадного соединения таких
полузвеньев, можно получить более сложные и качественные фильтры, например,
полные Т и П – образные звенья, рис. 3.79. Соединение полузвеньев
и звеньев производится по принципу идеального согласования внутри фильтра.
Характеристические сопротивления соединяемых частей должны быть одинаковы.
Поэтому такие фильтры иногда называют согласованными внутри.
В идеале мы хотели бы иметь такое полузвено, которое в
полосе пропускания имело бы активные и постоянные характеристические сопротивления
и не вносило бы совсем затухания (![]() ). Эти условия
обеспечить невозможно для такой схемы. Облегчим условия. Пусть
характеристические сопротивления будут просто активными, а затухание
отсутствует. Такие условия уже можно обеспечить с помощью чисто реактивных
элементов. Покажем это для ФНЧ.
). Эти условия
обеспечить невозможно для такой схемы. Облегчим условия. Пусть
характеристические сопротивления будут просто активными, а затухание
отсутствует. Такие условия уже можно обеспечить с помощью чисто реактивных
элементов. Покажем это для ФНЧ.
Коэффициент передачи делителя будет иметь частотную
зависимость, характерную для ФНЧ, если взять ![]() .
. ![]() являются обратными двухполюсниками,
являются обратными двухполюсниками, ![]() . Схема делителя изображена на рис. 3.80а.
Пусть
. Схема делителя изображена на рис. 3.80а.
Пусть ![]() . Тогда:
. Тогда: ![]() ;
; ![]() .
.
В полосе пропускания (![]() )
характеристические сопротивления активны, а последнее равенство будет
выполнено, если положить
)
характеристические сопротивления активны, а последнее равенство будет
выполнено, если положить ![]() . Таким образом,
сформулированные облегчённые условия реализуются. В полосе задерживания (
. Таким образом,
сформулированные облегчённые условия реализуются. В полосе задерживания (![]() ) характеристические сопротивления
становятся реактивными, а
) характеристические сопротивления
становятся реактивными, а ![]() . Эти зависимости
изображены на рис. 3.80.
. Эти зависимости
изображены на рис. 3.80.
В качестве примера рассмотрим симметричный ФНЧ пятого порядка, состоящий из двух Т – образных звеньев (4 полузвена), рис. 3.81а, и оценим его возможности. Фильтры такого типа обязательно должны быть нагружены на сопротивления, близкие к характеристическим, желательно даже с двух сторон, чтобы не проявлялись резонансы.
В идеале должно быть 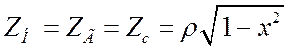 . Тогда
. Тогда
![]() . Но характеристическое сопротивление, к сожалению,
точно не реализовать. Чаще всего встречается ситуация, когда
. Но характеристическое сопротивление, к сожалению,
точно не реализовать. Чаще всего встречается ситуация, когда ![]() . Это даёт идеальное согласование на
нулевой частоте, для постоянной составляющей. Практически согласование
оказывается достаточно хорошим в полосе частот до
. Это даёт идеальное согласование на
нулевой частоте, для постоянной составляющей. Практически согласование
оказывается достаточно хорошим в полосе частот до ![]() .
Приведённый рис. 3.81б наглядно иллюстрирует роль согласования. Первая кривая
соответствует идеальному согласованию,
.
Приведённый рис. 3.81б наглядно иллюстрирует роль согласования. Первая кривая
соответствует идеальному согласованию, ![]() . Вторая
кривая даёт коэффициент передачи для реальной ситуации,
. Вторая
кривая даёт коэффициент передачи для реальной ситуации, ![]() .
Для сравнения приведена ещё характеристика фильтра Баттерворса пятого порядка.
Для него
.
Для сравнения приведена ещё характеристика фильтра Баттерворса пятого порядка.
Для него 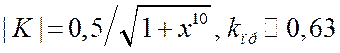 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.