Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 10

Выразим характеристические сопротивления через элементы матрицы , привлекая необходимые формулы (3.20) и (3.24).

  .

В итоге: 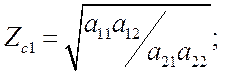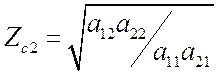.                                       (3.29)

 называют характеристическим сопротивлением со стороны входа (входное), а  - со стороны выхода (выходное). Для симметричного 4 ^х-пол.  и, следовательно, .

Покажем важное свойство характеристических сопротивлений. Если , то . Если , то . В самом деле, пусть . Тогда .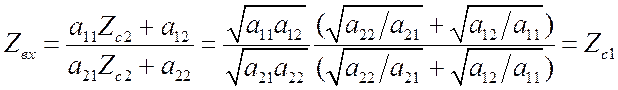

Условие  и есть условие согласования сопротивлений, при котором реализуется минимальное ослабление сигнала. Это мы обсудим немного позже на примерах.

Теперь выразим характеристическую постоянную для прямого направления передачи. . Преобразуем сначала произведение , привлекая систему уравнений с матрицей  и выражение для .

.

В итоге, 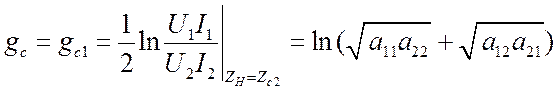.                        (3.30)

Если аккуратно вычислить  для обратного направления передачи, то мы получим . Для обратимого 4 ^х-пол. , поэтому достаточно ввести одну постоянную передачи . В общем случае , или . Есть основания говорить, что отличие  от единицы определяет меру (степень) необратимости.

В заключение, выразим элементы матрицы  (а следовательно и любой другой) через характеристические параметры обратимого 4 ^х-пол. Напишем цепочку равенств, из которых будет следовать результат.  , т.к. ; . В результате:

.                 (3.31)

Если , то  - симметрия. .

3.6.8.  Рабочие параметры. Вносимое затухание.

Характеристическая постоянная передачи получается при условии согласования (), которое чаще всего реализовать не удаётся. Поэтому в реальных условиях определяются рабочие характеристики, одной из которых является вносимое затухание (вносимая постоянная передачи). Оно определяется путём сравнения двух схем подключения нагрузки к генератору, непосредственно, как на рис. 3.4, и через четырёхполюсник, как на рис. 3.14. Вносимое затухание 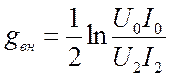. Здесь: .  есть мощность в нагрузке при непосредственном подключении нагрузки к генератору, а  есть мощность в нагрузке во второй схеме. Свяжем  и .

. Используя это равенство, получим 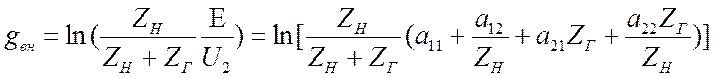.      (3.32)

Выразив элементы матрицы  через характеристические параметры и сделав необходимые преобразования, можно получить следующее выражение.

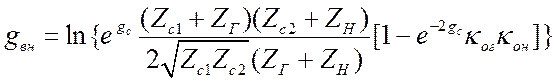.                                         (3.33)

Здесь  и  есть коэффициенты «отражения» (рассогласования) на входе и выходе. Они обращаются в ноль при условии согласования.

Что даёт нам вносимое затухание? Казалось бы, эта величина определена очень формально и абстрактно. Однако это не так. Из равенства (3.32) имеем:

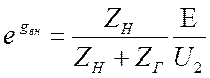. Отсюда 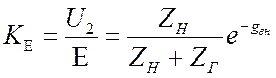.                                  (3.34)

Если , тогда . Таким образом, вносимое затухание непосредственно связано с коэффициентом передачи , важной характеристикой 4 ^х-пол. Вносимое затухание, так же как и , есть комплексная величина. . При этом,  () определяет собственно затухание, ослабление амплитуды, в то время как  даёт сдвиг фазы.

3.6.9.  Общие формулы для параметров четырёхполюсника.

Выразим стационарные параметры 4 ^х-пол. через характеристические, причём приведём просто сводку формул, почти без комментариев.

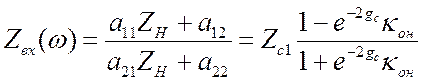.                                                           (3.35)

Отсюда можно получить интересное равенство, определяющее рассогласование на входе. .

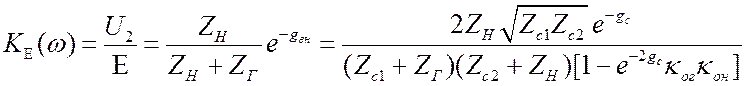.              (3.36)

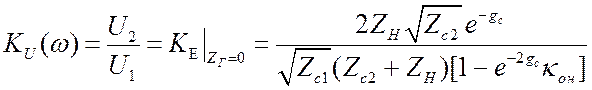.                                    (3.37)

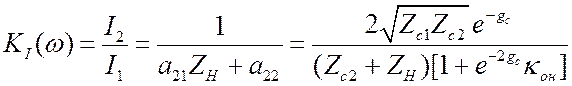.                                       (3.38)

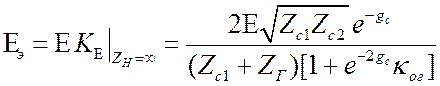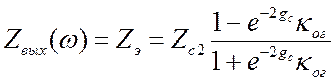. .       (3.39)

Если , то: .

3.7. Фильтры. Классификация. Терминология.

Электрические фильтры находят чрезвычайно широкое применение. Без фильтров не сделать ни одного стоящего устройства. Все приёмники, телевизоры содержат множество самых разнообразных фильтров, простых и сложных. Классический пример использования фильтров – это передача нескольких сигналов одновременно по одному кабелю, линии. Они передаются на разных частотах. В приёмном устройстве их разделяют с помощью фильтров.