Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 6

Решаем ту же задачу, но теперь без спектров. Считаем заданной импульсную или переходную характеристику. Пусть  при . Представим входной сигнал в виде суммы. 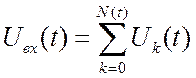, где  есть очень короткие прямоугольные импульсы длительности , амплитуда которых пропорциональна , рис. 3.15.  ( - целая часть ). Определим импульс , который отличается от импульса  только тем, что он имеет единичную амплитуду. Тогда все импульсы  получаются из импульса  путём изменения амплитуды и сдвига. ; …...

Длительность импульсов  надо задать так, чтобы в полосе частот, определяемой коэффициентом передачи, спектр этих импульсов был равномерным (как у ). Тогда реакцией цепи на каждый такой импульс будет импульсная характеристика , умноженная на «площадь» импульса и смещённая на соответствующее время. …. . Суммируя эти реакции на выходе, получим 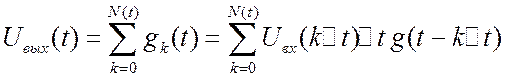. Теперь совершим предельный переход  () и получим интеграл вместо суммы ().

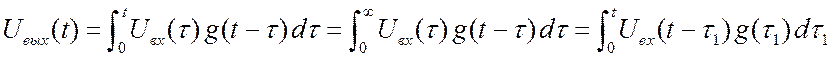. (3.13)

Обе подынтегральные функции равноправны. Верхний предел часто пишут бесконечным, поскольку , когда .

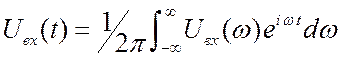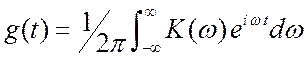Приведённый результат легко получить и на основе спектрального подхода. Если учесть, что  и , то 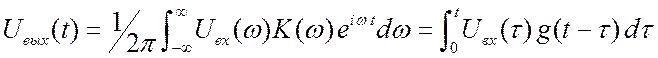. Обратное преобразование Фурье от произведения спектральных функции равно свёртке временных.

Можно выразить выходное напряжение суперпозицией переходных характеристик и получить следующее выражение, которое часто называют формулой Дюамеля. 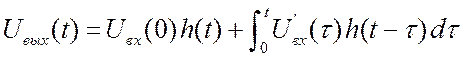.                                        (3.14)
К ней мы придём, используя такие рассуждения. Снова 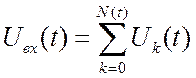, но теперь  это ступенчатые функции, рис. 3.16.  , т.к.  есть «высота» следующей ступеньки.  и т.д. Реакция на каждую функцию  есть . Суммируя эти реакции на выходе, будем иметь: 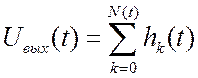, где . После выделения первого члена суммы и предельного перехода к интегралу, получим приведённый результат. Он так же легко получается со спектральных позиций.

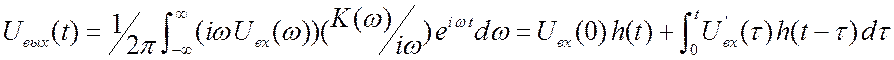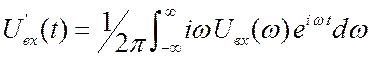. Здесь мы учли, что  ( есть оператор дифференцирования), а 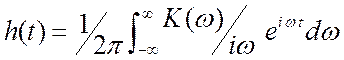. Реакцию на начальный скачок входного напряжения обычно выделяют из интеграла, хотя можно этого и не делать.

Приведённые интегралы составляют основу временного подхода и позволяют найти реакцию 4 ^х-пол. на любое воздействие по импульсной или переходной характеристике. Следует отметить, что разделение методов анализа на спектральные и временные в значительной степени условно. Всё сводится к тому, какой считать интеграл, Фурье или свёртку.

Примеры применения общих методов анализа мы рассмотрим немного позже. Перейдём к задаче определения параметров 4 ^х-пол., и, прежде всего, .

3.6. Матричная теория линейных четырёхполюсников.

Постулируем зависимость от времени . Рассмотрим линейные пассивные 4 ^х-пол. Стандартное направление токов и напряжений указано на рис. 3.17. Пусть 4 ^х-пол. имеет k независимых контуров. Первый контур выберем для входной цепи, второй – для выходной. Все остальные внутри. Токи входных зажимов одинаковы. Напишем систему уравнений контурных токов.

                                                                      (3.15)

   ………………………………

Нас не интересуют процессы внутри 4 ^х-пол. Нам надо связать входные переменные () и выходные (). Напряжения считаем заданными. Пишем решение системы для токов. 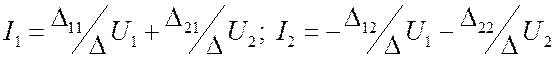 . Здесь  есть главный определитель системы, а  - миноры. Введём обозначения: . В итоге получили систему линейных уравнений 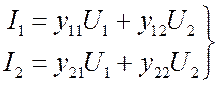, или короче 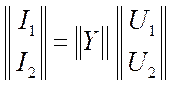.    (3.16)

Четыре элемента  образуют матрицу проводимостей , которая полностью определяет свойства рассматриваемого 4 ^х-пол. Элементы матрицы не зависят от амплитуд токов и напряжений.

3.6.1. Другие системы уравнений.

Мы имеем четыре переменные, две входные и две выходные. Если любые две из них принять за независимые, то две другие окажутся зависимыми. Тогда можно написать всего 6 равноправных систем. Для всех систем направления токов и напряжений одинаково. Одна уже была написана. Выпишем ещё 4.

.

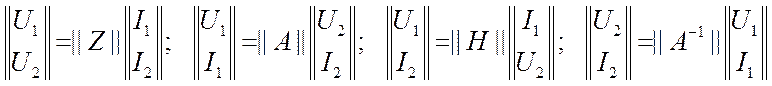Последний вариант уже очевиден. Он используется крайне редко. Три матрицы,  и , можно назвать прямыми, а другие три – обратными. Для перехода к обратной матрице надо: 1. Элементы на главной диагонали поменять местами; 2. Поменять знаки у двух других элементов; 3. Поделить все элементы на определитель системы. Например, матрица сопротивлений