Отметим ещё одно интересное обстоятельство. Сигнал ![]() оказывается как бы задержанным на
некоторое время. Часто время задержки определяют условно, как время нарастания
сигнала до половины установившегося значения. По рисунку можно оценить, что
оказывается как бы задержанным на
некоторое время. Часто время задержки определяют условно, как время нарастания
сигнала до половины установившегося значения. По рисунку можно оценить, что ![]() (точнее 1,44) для значения
(точнее 1,44) для значения ![]() . При этом фазовая характеристика
достаточно линейна в полосе пропускания (близка к оптимальной). Если теперь
время задержки определить по наклону фазовой характеристики при
. При этом фазовая характеристика
достаточно линейна в полосе пропускания (близка к оптимальной). Если теперь
время задержки определить по наклону фазовой характеристики при ![]() , то мы получим
, то мы получим ![]() .
Совсем неплохое совпадение.
.
Совсем неплохое совпадение.
3.9.4. Последовательный колебательный контур как полосовой фильтр.
Обычно выходное напряжение снимается с конденсатора,
рис 3.63, поэтому схема такая же, как и для ФНЧ. Только теперь ![]() и самым удобным выражением для анализа
коэффициента передачи становится следующее:
и самым удобным выражением для анализа
коэффициента передачи становится следующее: ![]() , если
, если ![]() . Наибольший интерес представляет поведение
коэффициента передачи вблизи резонансной частоты
. Наибольший интерес представляет поведение
коэффициента передачи вблизи резонансной частоты ![]() , где он
меняется очень резко, за счёт множителя
, где он
меняется очень резко, за счёт множителя ![]() в
знаменателе.
в
знаменателе.
Будем
считать расстройку малой, ![]() . Тогда
. Тогда ![]() и
и ![]() .
Поэтому множитель
.
Поэтому множитель ![]() в знаменателе выражения для
в знаменателе выражения для ![]() часто опускают.
часто опускают. 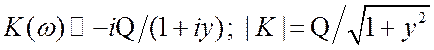 ;
;
![]() . (3.55) Типичные зависимости модуля и
аргумента коэффициента передачи приведены на рис. 3.63 для двух значений
. (3.55) Типичные зависимости модуля и
аргумента коэффициента передачи приведены на рис. 3.63 для двух значений ![]() . Граничные частоты полосы пропускания получаются,
когда
. Граничные частоты полосы пропускания получаются,
когда ![]() , т.е.
, т.е. ![]() . Так
экспериментально, по полосе, определяют добротность контура. Чем больше
добротность контура, тем ýже полоса пропускания.
. Так
экспериментально, по полосе, определяют добротность контура. Чем больше
добротность контура, тем ýже полоса пропускания.
При резонансе выходное напряжение в ![]() раз больше входного, но сопротивление
контура мало (
раз больше входного, но сопротивление
контура мало (![]() ). Генератор должен это терпеть.
Таким образом, последовательный колебательный контур с большой добротностью
даёт узкополосный полосовой фильтр. Однако качество фильтра оказывается низким.
Так, при
). Генератор должен это терпеть.
Таким образом, последовательный колебательный контур с большой добротностью
даёт узкополосный полосовой фильтр. Однако качество фильтра оказывается низким.
Так, при ![]() , а требуется часто 0,7-0,8. Приведём
пример.
, а требуется часто 0,7-0,8. Приведём
пример.
Пусть контур приёмника настроен на частоту ![]() мГц и
мГц и ![]() . Тогда
полоса пропускания фильтра
. Тогда
полоса пропускания фильтра ![]() кГц. При расстройке на
10 кГц относительно
кГц. При расстройке на
10 кГц относительно ![]() ,
, ![]() уменьшается
до уровня 0,71 (
уменьшается
до уровня 0,71 (![]() , граница полосы пропускания).
При расстройке на 20 кГц (
, граница полосы пропускания).
При расстройке на 20 кГц (![]() ),
), ![]() . Это очень плохо. Реальное ослабление
сигнала при такой расстройке должно составлять десятки, и даже сотни, раз.
Свойство приёмника подавлять сигналы соседних станций называют избирательностью
по соседнему каналу. Она определяется отношением
. Это очень плохо. Реальное ослабление
сигнала при такой расстройке должно составлять десятки, и даже сотни, раз.
Свойство приёмника подавлять сигналы соседних станций называют избирательностью
по соседнему каналу. Она определяется отношением ![]() при
заданной расстройке
при
заданной расстройке ![]() . Избирательность часто выражают
в логарифмических единицах, децибеллах. Приводят не само отношение, а величину
. Избирательность часто выражают
в логарифмических единицах, децибеллах. Приводят не само отношение, а величину ![]() . Если
. Если ![]() , то
, то ![]() дБ; если
дБ; если ![]() , то
, то ![]() дБ. Типичная избирательность приёмников по
соседнему каналу составляет 40-50 дб при расстройке на 10 кГц.
дБ. Типичная избирательность приёмников по
соседнему каналу составляет 40-50 дб при расстройке на 10 кГц.
К вопросу улучшения качества полосовых фильтров мы ещё вернёмся.
3.9.5. Переходные процессы в последовательном колебательном контуре с большой добротностью.
Переходную характеристику последовательного контура мы
уже вычисляли. Воспользуемся выражением (3.54) и примем добротность контура ![]() . Тогда:
. Тогда: 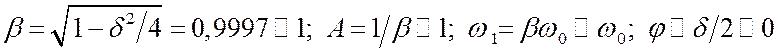 . В итоге
имеем
. В итоге
имеем ![]() . Получился типичный колебательный процесс
установления к стационарному значению, представленный на рис. 3.64. Амплитуда
колебаний уменьшится в 10 раз, когда
. Получился типичный колебательный процесс
установления к стационарному значению, представленный на рис. 3.64. Амплитуда
колебаний уменьшится в 10 раз, когда ![]() . Отсюда
. Отсюда ![]() , где T есть период
колебаний. Контур «звучит» на частоте
, где T есть период
колебаний. Контур «звучит» на частоте ![]() . Однако
при большой добротности контура различие между
. Однако
при большой добротности контура различие между ![]() и
и ![]() столь мало, что практически его не
учитывают.
столь мало, что практически его не
учитывают.
Отметим одну интересную возможность, которой пользуются на практике. Через индуктивность можно зарядить ёмкость почти до удвоенного напряжения источника. Чтобы ёмкость не разряжалась, ставят в цепь заряда диод.
Вычислим теперь реакцию контура с большой добротностью
на длинный радиоимпульс, при условии, что контур настроен на частоту сигнала (![]() ). Пусть
). Пусть ![]() .
Тогда:
.
Тогда: 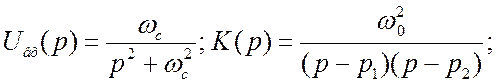
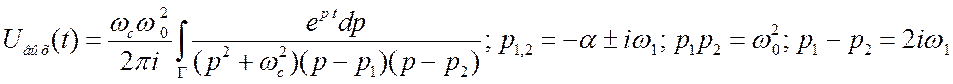 . Мы
имеем 4 полюса (две комплексно сопряжённые пары). Два полюса за счёт входного
сигнала,
. Мы
имеем 4 полюса (две комплексно сопряжённые пары). Два полюса за счёт входного
сигнала,![]() , находятся на мнимой оси плоскости p. Им соответствуют незатухающие вычеты
, находятся на мнимой оси плоскости p. Им соответствуют незатухающие вычеты ![]() , которые в сумме дают стационарный процесс
, которые в сумме дают стационарный процесс
![]() (
(![]() ). Он
останется при
). Он
останется при ![]() , когда переходные процессы
закончатся. Эту часть решения обычно пишут сразу, как реакцию контура на
гармонический сигнал.
, когда переходные процессы
закончатся. Эту часть решения обычно пишут сразу, как реакцию контура на
гармонический сигнал.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.