Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 23

Коэффициент передачи при параллельном подключении генератора отличается от последовательного лишь медленно меняющимся множителем в знаменателе, который мало меняет ситуацию. Общий характер зависимостей сохраняется, в частности, и зависимость от величины связи. Получается несколько бóльшая разница в величинах максимумов , когда связь больше критической, и дополнительный фазовый сдвиг на . Максимумы  легко сделать одинаковыми, изменив немного резонансные частоты контуров (так обычно и делают).

Рассмотренные системы из двух связанных контуров находят очень широкое применение на практике (приёмники, телевизоры, аппаратура связи и др.). Обычно реализуется связь больше критической. Однако два связанных контура не обеспечивают требуемое практикой качество фильтров. Приходится ещё усложнять колебательную систему. В качестве примера на рис. 3.75а приведена схема полосового фильтра приёмника второго класса «ВЭФ 202». Фильтр состоит из четырёх связанных контуров с ёмкостной связью между ними. Контура могут быть не одинаковы, но настроены на одну частоту. Анализ ёмкостной связи приводит к аналогичным зависимостям. На рис. 3.75б изображён ещё один распространённый вариант полосового фильтра из четырёх связанных контуров. Фильтр имеет две пары контуров с индуктивной связью, между которыми реализована ёмкостная связь. В телевизорах используют ещё более сложные колебательные системы, содержащие порядка десятка контуров.

3.9.11. Фазовращатели.

Нередко возникает необходимость скорректировать фазовую характеристику цепи, по возможности не затрагивая амплитудную. Такие цепи существуют. Рассмотрим два примера мостовых цепей.

1. RC цепь, рис. 3.76а. Будем считать , тогда токи в ветвях одинаковы. , где . В итоге: .    (3.63) Этот результат можно получить, ничего не вычисляя. Надо просто нарисовать векторную диаграмму, построив прямоугольник со сторонами  и . Входное и выходное напряжения есть диагонали прямоугольника.

2. LC цепь, рис. 3.76б. О входном сопротивлении этой цепи, как двухполюсника, уже шла речь. Определим теперь её коэффициент передачи. При этом мы можем воспользоваться формулами для мостовой цепи, приведёнными в начале этой главы, или готовыми формулами для  и , выраженными через элементы матрицы. Второй путь проще. Матрица  A  такой цепи была приведена ранее, матрица (3.28). Для этого примера:  и  есть обратные двухполюсники; ; ; . Тогда: . В результате:  .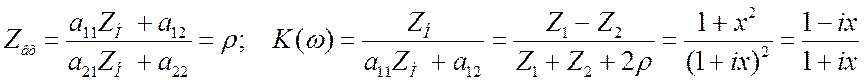

Оказалось, что коэффициент передачи для двух цепей одинаков. Однако вторая цепь обладает очень важным преимуществом. Характеристическое сопротивление LC цепи активно и постоянно, . Эту цепь можно идеально согласовать в широкой полосе частот и эффективно передавать мощность в нагрузку почти без потерь.

Недостаток обеих цепей состоит в том, что они уравновешены, симметричны относительно продольной «оси» четырёхполюсника (можно поменять местами верхние и нижние выводы). Для таких цепей и входные, и выходные выводы должны быть равноправны (симметричны) по отношению к общему проводу (земле). Нагрузка уравновешенных цепей тоже должна быть уравновешенной.

Подавляющее большинство цепей (все приведённые ранее примеры) неуравновешенны. Они фактически являются трёхполюсниками, поскольку нижние выводы, входной и выходной, соединены накоротко (общий провод, земля). Совместное использование уравновешенных и неуравновешенных цепей требует специальных «симметрирующих» устройств, в качестве которых часто используются трансформаторы. Типичное решение этой проблемы показано на рис. 3.77. Если мы соединим эти два четырёхполюсника без симметрирующего устройства, то нарушится симметрия схемы фазовращателя.

3.10. Реактивные фильтры. Общие соображения. Роль согласования.