Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 15

Все переходные характеристики рассмотренных цепей второго порядка связаны простой зависимостью. Чтобы убедиться в этом, надо сравнить числители коэффициентов передачи. Для ФНЧ это единица, для полосовых – , для ФВЧ – . Если теперь вспомнить, что  (или ) есть оператор дифференцирования, то связь становится очевидной.

Определим сначала переходную характеристику двухзвенного ФНЧ с одинаковыми звеньями (), используя преобразование Лапласа. Будем следовать намеченной ранее программе действий для спектрального метода анализа, заменяя на каждом шаге  на , или на . В данном случае .

1. . Напомним, что это обобщённый спектр. В этом случае преобразование Лапласа надёжнее.

2. 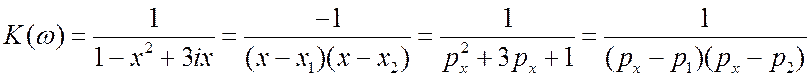. ;. Корни получились порядка единицы. В этом проявляется удобство, преимущество безразмерных (относительных) частот.

3. .

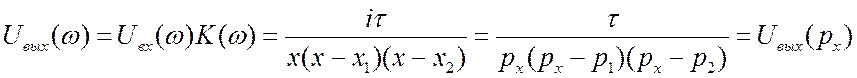4. .

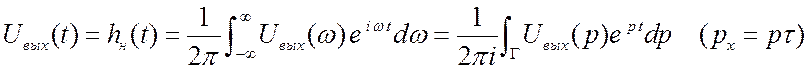Контур  проводится правее всех особенностей подынтегральной функции (ниже всех особенностей для преобразования Фурье). Подынтегральная функция имеет три простых полюса.  за счёт  и два вещественных,  и , за счёт . Интеграл будем вычислять по вычетам.

Рассуждают так. Пусть , тогда к исходному контуру  добавляем полуокружность очень большого радиуса  в правой полуплоскости , т.к. интеграл по этой полуокружности равен нулю при  (лемма Жордана). Получаем замкнутый контур, рис. 3.49г, внутри которого нет особенностей подынтегральной функции. Значит  при . Пусть теперь . Добавляем полуокружность большого радиуса в левой полуплоскости, т.к. интеграл по этой полуокружности равен нулю. Опять получаем замкнутый контур, рис. 3.49в, но теперь внутри него есть три полюса. Интеграл равен .

Напомним формулы из курса математики для определения вычетов.  Если подынтегральная функция в окрестности простого полюса    имеет вид , то вычет . Если функция представлена в виде отношения , причём  (но ), то . Наконец, для полюса второй кратности, когда функция имеет вид ,.

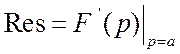Используя эти формулы, получим переходную характеристику для ФНЧ.

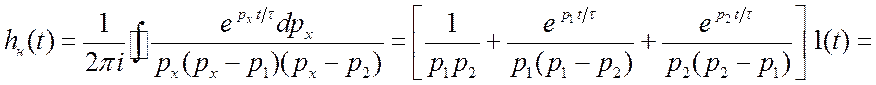
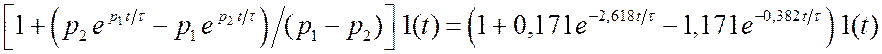. (3.47) Она изображена на рис. 3.50. Можно показать, разлагая exp в ряды, что, при . В этом временном интервале цепь осуществляет двукратное интегрирование. Переходная характеристика при  получается непрерывная и гладкая. При , . Время установления (время нарастания сигнала от уровня 0,1 до уровня 0,9) для двухзвенной цепи значительно больше, чем для одного звена, и равно приблизительно .

Чтобы получить переходную характеристику полосового фильтра (и цепи Вина) при , надо вычислить производную от  (по безразмерной переменной ). Будем иметь, рис. 3.51: .     (3.48) Имеем сравнительно быстрое нарастание напряжения на выходе и медленный спад. Максимальное напряжение достигается при .

Переходная характеристика для ФВЧ получится, если снова взять производную, но теперь от . .                       (3.49) Результат изображён на рис. 3.52. Входной скачок напряжения цепь воспроизводит без искажения (цепь идеализирована). Затем напряжение на выходе быстро уменьшается и даже меняет знак. Попробуйте объяснить это с физических позиций.

3.8.7.1.  Переходная характеристика ПФ при условии .

В силу важности этого случая, мы рассмотрим его отдельно. Примем условия, сформулированные при анализе коэффициента передачи. Пусть: , причём неравенство очень сильное, например, ; . Вычислим приближённо корни характеристического уравнения , разлагая радикал в ряд, поскольку . . 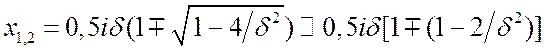. Воспользуемся преобразованием Фурье. . .

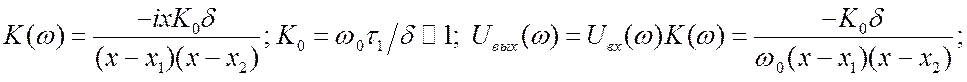
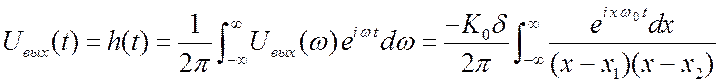Интеграл будем считать по вычетам.  при . Это очевидно. Пусть . Превращаем контур в замкнутый, добавляя полуокружность в верхней полуплоскости . Внутри контура оказываются два полюса. Суммируя вычеты, получим .                          (3.50)

Здесь мы учли приближенные равенства: . Результат изображён на рис 3.53 в двух вариантах, с разными масштабами времени, при условии . Слева представлено начало переходной характеристики при . Тогда ; всё как в интегрирующей цепочке с постоянной времени . Длительность фронта составляет . Однако, уже здесь заметно уменьшение напряжения за счёт дифференцирующей цепи. Это уменьшение более чётко проявляется на правом рисунке, поскольку , при . Здесь мы имеем типичное «дифференцирование».