Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 25

При идеальном согласовании фильтр в полосе пропускания совсем не вносит затухания. В реальной ситуации фильтр вносит затухание, но оно незначительно, пока согласование достаточно хорошее. Только при подходе к граничной частоте, где характеристическое сопротивление начинает меняться сильно, возникает значительное рассогласование, и затухание быстро увеличивается. Наличие потерь в реактивных элементах фильтра приводит к дополнительному ослаблению сигнала.

Существуют справочники по фильтрам, в которых приводятся уже готовые результаты расчётов фильтров разных классов. Достаточно задать сопротивление нагрузки, граничную частоту и порядок фильтра, чтобы определить значения элементов согласованного фильтра, фильтра Баттерворса и др. Практика нередко ставит очень жёсткие условия и приходится делать фильтры 8 - 10 порядков.

Перейдём к фильтрам других типов. Полузвено ФВЧ получится, если поменять местами элементы L и C, рис. 3.82а. Теперь: ;    . Все формулы для ФВЧ, получаются  из приведённых для ФНЧ, путём частотного преобразования. Надо  заменить на . Например, .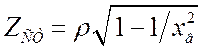

Полосовой фильтр получится, если вместо L и C  в фильтр НЧ, мы поставим колебательные контура, последовательный и параллельный, рис. 3.82б, настроенные на одну частоту . Теперь: ;  ;  ; , где .

Коэффициент передачи максимален на резонансной частоте контуров. Эта частота будет соответствовать , если сделать замену . Параметр  определяет полосу пропускания полосового фильтра. Он может быть и широкополосным. Чем меньше , тем шире полоса.

Режекторный фильтр получится, если поменять местами контура, рис. 3.82в. Преобразование частоты от ФНЧ таково: .  соответствует . Таким образом можно получить качественные фильтры разных типов.

Некоторые новые возможности открываются при использовании активных фильтров (фильтров с усилителями) и цифровых фильтров. Последние реализуются с помощью ЭВМ при обработке дискретных сигналов. Эти новые возможности мы обсудим позже.

3.11. Некоторые итоги. Физическая осуществимость цепей.

В заключение этой главы обсудим ещё раз некоторые общие свойства характеристик четырёхполюсников и критерии физической осуществимости цепей.

Начнём с входного сопротивления. Для пассивного четырёхполюсника  есть комплексная дробно - рациональная функция частоты, отношение двух полиномов, причём степени полиномов не могут отличаться больше, чем на единицу.  являются чётными функциями частоты, а - нечётные.  определяет отношение амплитуд напряжения и тока, а - сдвиг фаз между ними. Пассивная цепь может только потреблять энергию от генератора (источника), поэтому . Равенства достигаются только для идеализированной цепи без потерь.

Любая цепь, содержащая реактивные элементы, проявляет себя при  или как индуктивность, или как ёмкость. Поэтому  либо стремиться к нулю, либо – к бесконечности. Иначе, , где . Знаменатель всегда можно сделать чётной функцией частоты, тогда числитель будет нечётным. На резонансных частотах . Различают последовательные резонансы (малое сопротивление) и параллельные (большое). В сложных цепях, содержащих реактивные элементы большой добротности, эти резонансы чередуются.

Аналогичные соображения можно высказать и относительно выходного сопротивления, поскольку оно есть входное сопротивление при обратном направлении передачи сигнала.

Перейдём к коэффициенту передачи. Для любой реальной пассивной цепи  есть тоже комплексная дробно – рациональная функция частоты, отношение двух полиномов. Но теперь , поскольку , когда . Только для некоторых «идеализированных» цепей (дифференцирующая цепь, ФВЧ) степени могут быть одинаковыми, так как мы, фактически, не учитываем ёмкость нагрузки и сопротивление генератора.  определяет отношение амплитуд напряжений на входе и выходе и является чётной функцией частоты, а определяет сдвиг фаз напряжений и является нечётной функцией.