Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 5

3. Симметричные и несимметричные. У симметричных можно поменять местами вход и выход. Все напряжения и токи при этом останутся прежними. Имеется в виду симметрия относительно «поперечной» оси 4 ^х-пол (вертикальной).

4. Уравновешенные и неуравновешенные. У первых можно поменять местами верхние и нижние зажимы без каких-либо изменений. Здесь речь идёт о симметрии относительно «продольной» оси 4 ^х-пол.

Часто используется понятие эквивалентности 4 ^х-пол. Два 4 ^х-пол. называют эквивалентными, если один из них мы можем заменить другим. При этом токи в цепях генератора и нагрузки не должны измениться.

В этой главе мы будем рассматривать линейные пассивные 4 ^х-пол. Они подчиняются принципу обратимости (взаимности).

3.5.1.  Параметры четырёхполюсников.

Сначала перечислим параметры 4 ^х-пол. для гармонического сигнала .

1. Входное сопротивление . Оно зависит от режима на выходе, от .

2. Выходное сопротивление. Для определения  весь 4 ^х-пол. вместе с генератором рассматривают как активный двухполюсник и заменяют эквивалентным генератором, т.е. переходят к схеме, изображённой на рис. 3.3б. ЭДС эквивалентного генератора , где  - напряжение на выходе 4 ^х-пол., когда  (холостой режим), а  представляет входное сопротивление
4 ^х-пол. со стороны выхода, когда . Это и есть выходное сопротивление
4 ^х-пол. Оно зависит от . Часто используют формулу (3.4) и пишут , где  - ток на выходе 4 ^х-пол. при его коротком замыкании.

3. Коэффициент передачи. Различают коэффициенты передачи по напряжению, по току и по мощности.. Чаще всего используется коэффициент передачи по напряжению.

Все перечисленные параметры для линейных 4 ^х-пол. не зависят от амплитуды входного сигнала.

Для негармонического сигнала свойства 4 ^х-пол. полностью определяются импульсной или переходной характеристикой. Импульсная характеристика  является реакцией 4 ^х-пол. на очень короткий прямоугольный импульс единичной «площади» (в пределе ). Переходная характеристика  есть реакция 4 ^х-пол. на единичный скачок напряжения, .

Сейчас мы увидим, что, зная  или , можно вычислить реакцию
4 ^х-пол. на любое другое воздействие.

3.5.2. Общие методы анализа линейных 4 ^х-пол. Спектральный подход.

Типичная задача анализа цепи заключается в определении  по заданному . Эту задачу мы и рассмотрим. При этом ради простоты, будем считать . Позже мы получим выражения, учитывающие это сопротивление.

Последовательность решения указанной задачи при спектральном подходе такова.

1. Определяем коэффициент передачи 4 ^х-пол. по напряжению . Для краткости будем опускать значок «U», когда мы имеем дело с коэффициентом передачи по напряжению.

2. Разлагаем  на спектральные составляющие и определяем спектр 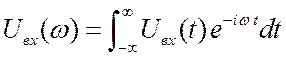 (или ).

3. Находим спектр сигнала на выходе .

4. Находим сигнал на выходе, выполняя обратное преобразование Фурье

.

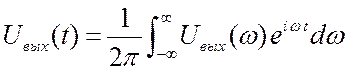Обычно подынтегральная функция имеет только полюса на комплексной плоскости , и интеграл вычисляется с помощью теоремы о вычетах.

Учитывая написанное, становится ясна роль гармонических сигналов и . Коэффициент передачи  полностью характеризует данный 4 ^х-пол. и позволяет найти реакцию на любое воздействие. Никакого дифференциального уравнения составлять и решать не надо.

В качестве примера, найдем импульсную и переходную характеристики. Пусть . Тогда  (спектр обобщённый) и выходное напряжение 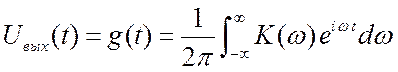 .                                                        (3.11)

Из этого равенства следует, что  и  связаны преобразованием Фурье. Обе эти функции одинаково представляют специфику данного 4 ^х-пол.

Если , то . Эти равенства отражают важное свойство линейной цепи, инвариантность сдвига (запаздывания).

Пусть теперь . Тогда  (спектр обобщённый). Переходная характеристика 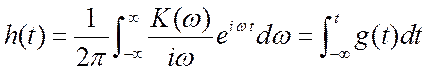(),   (3.12) поскольку .

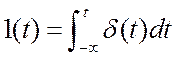Вместо преобразования Фурье часто используют преобразование Лапласа.

3.5.3.  Общие методы.  Временной подход.