В качестве примера, наглядно иллюстрирующего
возможности такого способа, рассмотрим связанные колебательные контура.
Характер связи может быть различным. Чаще используются индуктивные и ёмкостные
связи, рис. 3.67, хотя возможна и резистивная связь. Рассмотрим самую
распространённую схему индуктивной связи, рис. 3.67а. Начнём с вывода
коэффициента передачи цепи, содержащей трансформатор, рис. 3.68. ![]() есть взаимная индуктивность, а параметр
есть взаимная индуктивность, а параметр ![]() называют коэффициентом связи. Для обычных
трансформаторов связь обмоток сильная (за счёт сердечника) и
называют коэффициентом связи. Для обычных
трансформаторов связь обмоток сильная (за счёт сердечника) и ![]() . Для радиотехнических применений контуров
в качестве фильтров связь должна быть слабая,
. Для радиотехнических применений контуров
в качестве фильтров связь должна быть слабая, ![]() .
.
Пусть ![]() . Составим систему
уравнений Кирхгофа для двух связанных контуров.
. Составим систему
уравнений Кирхгофа для двух связанных контуров. ![]() . Из
второго уравнения находим связь токов.
. Из
второго уравнения находим связь токов. ![]() .
Исключая
.
Исключая ![]() из первого уравнения, получим
из первого уравнения, получим ![]() . Здесь
. Здесь ![]() есть
полное входное сопротивление первого контура (с учётом второго), а
есть
полное входное сопротивление первого контура (с учётом второго), а ![]() - вносимое сопротивление в первый контур
из второго. Далее,
- вносимое сопротивление в первый контур
из второго. Далее, ![]() . В итоге, коэффициент передачи
. В итоге, коэффициент передачи 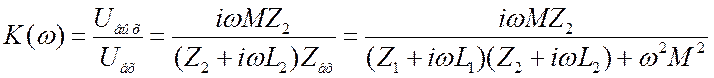 . (3.58)
. (3.58)
Эти выражения нам надо проанализировать. Но сначала отвлечёмся несколько от темы полосовых фильтров и напомним ситуацию с обычным трансформатором.
3.9.8. Трансформатор.
Примем следующие предположения: связь обмоток полная, ![]() ;
; ![]() ;
; ![]() есть коэффициент трансформации, а
есть коэффициент трансформации, а ![]() и
и ![]() -
количества витков обмоток. Фактически, мы рассматриваем идеальный
трансформатор, рис. 3.69а. Получим основные результаты.
-
количества витков обмоток. Фактически, мы рассматриваем идеальный
трансформатор, рис. 3.69а. Получим основные результаты.
1. Вносимое сопротивление имеет активную и реактивную
составляющие. ![]() ;
;
![]() ;
; ![]() (!).
(3.59)
(!).
(3.59)
2. Полное входное сопротивление ![]() стало активным и складывается из
собственного (
стало активным и складывается из
собственного (![]() ) и вносимого,
) и вносимого, ![]() . Именно так трансформируется сопротивление
нагрузки в первичную обмотку. Индуктивное сопротивление первичной обмотки
полностью скомпенсировалось за счёт вносимого. Сдвиг фаз между током и
напряжением отсутствует. Реализуются благоприятные условия для оптимальной
передачи мощности.
. Именно так трансформируется сопротивление
нагрузки в первичную обмотку. Индуктивное сопротивление первичной обмотки
полностью скомпенсировалось за счёт вносимого. Сдвиг фаз между током и
напряжением отсутствует. Реализуются благоприятные условия для оптимальной
передачи мощности.
Стоит разомкнуть вторичную обмотку (![]() ), и всё будет совсем иначе, как в катушке
с сердечником.
), и всё будет совсем иначе, как в катушке
с сердечником. ![]() . Главной теперь будет реактивная
составляющая сопротивления. Ток
. Главной теперь будет реактивная
составляющая сопротивления. Ток ![]() будет маленьким и
сдвинут по фазе к напряжению почти на
будет маленьким и
сдвинут по фазе к напряжению почти на ![]() .
Потребление мощности ничтожное. Это типичный режим холостого хода
трансформатора.
.
Потребление мощности ничтожное. Это типичный режим холостого хода
трансформатора.
3. Соотношение токов ![]() .
.
4. Выходное напряжение ![]() , если
, если ![]() .
. ![]() обычно
играет роль активного сопротивления первичной обмотки, поэтому написанное
неравенство реально выполняется.
обычно
играет роль активного сопротивления первичной обмотки, поэтому написанное
неравенство реально выполняется.
5. Мощность почти полностью передаётся во вторичную
обмотку, т.е. коэффициент полезного действия ![]() .
. ![]() .
.
Трансформаторы находят очень широкое применение в различных радиотехнических устройствах, где они выполняют две важные операции. Они трансформируют напряжения и токи, и согласуют сопротивления. Приведём наглядный пример применения трансформатора для согласования.
Пусть мы имеем источник переменного напряжения с ЭДС ![]() в и сопротивлением 100 ом, развивающим
мощность 1 вт. Сопротивление нагрузки 4 ома. Требуется передать в нагрузку
максимально возможную мощность. Оптимальная нагрузка для этого генератора
составляет 100 ом. В такую нагрузку он отдаст 0,5 вт. Если подключить заданную
нагрузку прямо к генератору, то будем иметь
в и сопротивлением 100 ом, развивающим
мощность 1 вт. Сопротивление нагрузки 4 ома. Требуется передать в нагрузку
максимально возможную мощность. Оптимальная нагрузка для этого генератора
составляет 100 ом. В такую нагрузку он отдаст 0,5 вт. Если подключить заданную
нагрузку прямо к генератору, то будем иметь ![]() вт.
Как передать в нагрузку бóльшую мощность? Ответ простой. Надо согласовать
сопротивление нагрузки и генератора с помощью трансформатора, рис. 3.69б, с
коэффициентом трансформации
вт.
Как передать в нагрузку бóльшую мощность? Ответ простой. Надо согласовать
сопротивление нагрузки и генератора с помощью трансформатора, рис. 3.69б, с
коэффициентом трансформации ![]() . Воспользуемся
приведёнными формулами.
. Воспользуемся
приведёнными формулами. ![]() ом;
ом; ![]() ом;
ом; ![]() а;
а; ![]() а;
а; ![]() в;
в; ![]() вт. Трансформатор выполнил свою роль.
вт. Трансформатор выполнил свою роль.
3.9.9. Связанные контура. Полосовой фильтр.
Контура
изображены на рис. 3.70. Связь слабая, ![]() .
Перечислим параметры контуров и переменные. Ниже приведены формулы только для
первого контура. Для второго всё аналогично, но со значком «2».
.
Перечислим параметры контуров и переменные. Ниже приведены формулы только для
первого контура. Для второго всё аналогично, но со значком «2». ![]()
![]()
![]() .
Перепишем теперь формулы пункта 3.9.7. с учётом этих обозначений.
.
Перепишем теперь формулы пункта 3.9.7. с учётом этих обозначений. ![]() . Вносимое сопротивление
. Вносимое сопротивление ![]() максимально при резонансе во втором контуре
(
максимально при резонансе во втором контуре
(![]() ). Входное сопротивление первого контура
). Входное сопротивление первого контура ![]() складывается из собственного и вносимого.
складывается из собственного и вносимого. ![]() . Выходное напряжение на рис. 3.70
снимается не со всего сопротивления
. Выходное напряжение на рис. 3.70
снимается не со всего сопротивления ![]() , а только с части (с
ёмкости), поэтому в это выражение введена коррекция.
, а только с части (с
ёмкости), поэтому в это выражение введена коррекция. ![]()
![]() . В итоге,
. В итоге, 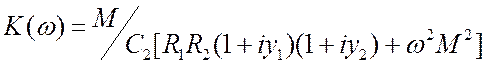 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.