Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 22

Эти общие выражения достаточно громоздкие, и обычно для упрощения анализа предполагают, что контура одинаковы. Это не абстрактная ситуация, такие системы находят широкое применение. Примем это предположение. Тогда мы просто опустим значки «1» и «2» у параметров и продолжим анализ. Введём новый безразмерный параметр связи , который называют степенью связи. При этом , а .

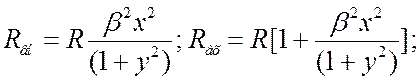
Будем считать добротность контуров большой и, прежде всего, выясним, как меняются вносимое и входное сопротивления при малых расстройках, когда . .  . 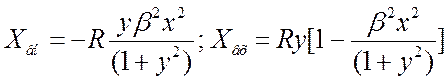(3.60) При анализе этих выражений x в числителе часто заменяют единицей. На резонансной частоте , , а . Если , то  только на частоте . Если же , то  обращается в ноль ещё на двух частотах, когда . Их называют частотами «связи». . . 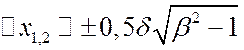Качественный характер поведения  при малых расстройках изображён на рис. 3.71. На частотах связи  оказывается меньше, чем на резонансной частоте .

Приведём итоговое выражение для коэффициента передачи двух одинаковых связанных контуров и обсудим результаты..    (3.61) 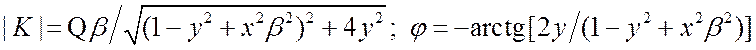.  максимален при  (для одиночного контура было ). На частотах связи . Зависимости  двух связанных контуров с добротностью 20 вблизи резонансной частоты для разных значений  приведены на рис. 3.72а. Контура одинаковы, их параметры не меняются. Меняется только связь. Обычно эти характеристики сравнивают с характеристикой одиночного контура, имеющего те же параметры. Она изображена пунктирной кривой и уменьшена в два раза ().

Если , то частотная характеристика системы очень похожа на пунктирную и получается, фактически, перемножением коэффициентов передачи отдельных контуров. Пусть . Тогда: . Связь называют критической, когда, поскольку при этом существенно меняется характер частотной зависимости параметров. При критической связи максимум ещё один. Полоса становится в 1,4 раза шире, . Усиление . Зато . Качество фильтра (избирательность) улучшилось. А это и есть главный эффект, ради чего мы стараемся.

Когда связь станет больше критической, , то зависимость  от частоты приобретает характерный вид с двумя максимумами на частотах связи. С ростом , их «разнос» увеличивается, полоса становится шире и растёт коэффициент прямоугольности. Рисунок это наглядно иллюстрирует. Максимальное значение  реализуется тогда, когда минимум на частоте достигнет уровня 0,7 от максимума. Практически это будет при значениях . При этом, полоса станет шире примерно в три раза, зато коэффициент прямоугольности достигнет значения 0,4.

Фазовые характеристики системы связанных контуров приведены на рис. 3.72б. Линейность фазовой характеристики в полосе пропускания фильтра с ростом , к сожалению, ухудшается.

Отметим ещё, что входное сопротивление, когда связь больше критической, минимально не на частоте , как для одиночного контура, а на некоторых частотах, близких к частотам связи. Собственное сопротивление первого контура по-прежнему минимально на резонансной частоте, но вносимое сопротивление больше и максимально. Поэтому  на частоте  имеет локальный максимум, причём этот максимум уже чётко проявляется даже при критической связи, когда  имеет один максимум.

3.9.10.  Связанные контура. Параллельное подключение.

Изобразим схему с генератором тока, рис. 3.73а. Как и для одиночного контура при таком включении, разница фактически будет только в сопротивлениях. Покажем это. Сначала мы пересчитаем сопротивление генератора в контур и упростим схему, как на рис. 3.73б. Здесь . Для этой схемы напишем систему уравнений, используя обозначения предыдущего параграфа. Ток генератора разветвляется по двум ветвям. ; . Из последнего уравнения выражаем  и исключаем его из второго уравнения. , где , как и раньше. Отсюда получаем связь всех остальных токов. . Переходим во второй контур. . Теперь напишем результат. 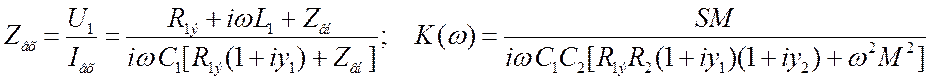. Анализ выражений проведём опять для одинаковых контуров (). . 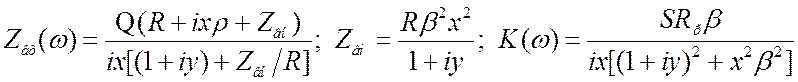     (3.62) Здесь . Входное сопротивление на частоте  комплексно. Резонансная частота получается немного меньше, чем . При этом . Сопротивление оказывается активным и максимальным, если . Если же  , то  имеет уже два максимума, а на частоте  реализуется локальный минимум. Характерный вид  от частоты приведён на рис. 3.74 для разных значений  при . Для критической связи уже есть заметный минимум.