Перспективы выявления и освоения месторождений газа, конденсата и нефти на шельфе морей России (Сборник научных трудов), страница 41

Экспериментальные исследования для плоского ребра показали, что изменение нормальных напряжений по боковой поверхности с глубиной в однородных песчаных грунтах происходит по линейному закону, а их величина достаточно близка к бытовому давлению [5], то есть;

а_п=К_ту-г-Я._о,                                          (8)

где К_т - коэффициент условий работы, принимаемый по табли­це; Х_о - горизонтальная составляющая коэффициента бокового давле­ния покоя с учетом "обратного" трения при ф^-ф.

Наименование грунта	Значение коэффициента Km
Плотный	1,0
Средней плотности	1,15
Рыхлый	1,3

В испытаниях при задавливании ребер среднее значение коэф­фициента трения грунта по боковой поверхности tg$ = ^т на разных глубинах погружения соответствовала значению тангенса угла внут­реннего трения грунта

96

Таким образом, после некоторых преобразований выражения (7) с учетом полученных экспериментальных данных, получим формулу для определения силы сопротивления задавливанию по боковой по­верхности плоского ребра в грунт многослойного основания:

Для клинообразного ребра в процессе экспериментов было ус­тановлено, что значение горизонтального давления а на боковую по­верхность зависит от перемещений грунта U и хорошо описывается выражением [5]:

а; . ■ и

о-_ч. =                          i  +^z₍,                                   (10)

;      !    су. .     \   \

где К_о j - начальный коэффициент отпора грунта на глубине Z,; Ui - горизонтальное переметение грунта на глубине Z,; а_пр, пре­дельное горизонтальное давление на ребро на глубине 7,\\ m коэф­фициент , характеризующий виды грунтов.

Сопротивление по боковой поверхности клинообразного ребра удобно рассчитывать методом послойного суммирования, тогда зави­симость (7) преобразуется в выражение

Значения общего сопрочивления задавливанию ребристых эле­ментов в грунт основания, определенные по формулам (5,8) и (5,10) соответственно для плоского и клинообразного ребра, показали хо­рошее соответствие значениям лабораторных и натурных экспери­ментов,

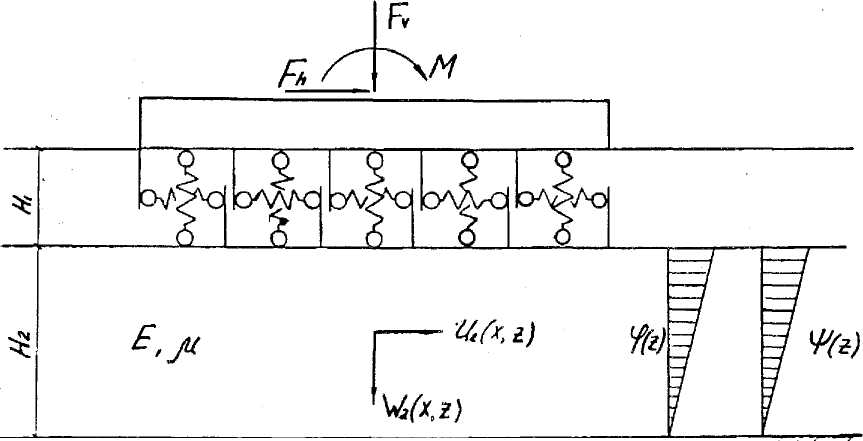
С целью определения напряженно-деформированного состояния основания гравитационного была разработана упругопластическая контактная модель [6], состоящая из комбинации двух слов (рис. 7): нижнего упругого слоя конечной толщины Н2 и верхнего уиругопла-стического слоя толщиной Н].

С целью разработки условий адаптации данной методики к рас­чету ребристых фундаментов ГП были проанализированы их конст­руктивные особенности и результаты экспериментальных исследова­ний, на основе которых было отмечено, что жесткость грунта, заклю-

97

ценного в межреберном пространстве, превышает жесткость нижеле­жащих слоев грунта.

Сделанное на этой основе допущение о том, что грунт в межре­берном пространстве - часть сооружения, повлекло за собой пониже­ние расчетной отметки плоскости контакта плиты с грунтом на глу­бину погружения ребер [7].

Данное обстоятельство влечет за собой следующие изменения в расчетной схеме:

-  грунтовое основание вокруг фундамента в уровне новой по­
дошвы оказывается пригруженным весом вышележащих слоев грунта
в виде пригрузки q (рис. 8);

-  в горизонтальную сопротивляемость фундамента оказывается
включенным пассивное давление грунта на передний ребристый эле­
мент;

-  вместе с тем, понижение уровня подошвы фундамента увели­
чивает плечо приложения горизонтальной силы, что приводит к
ухудшению его работы (в частности по зависимости момент - крен).