Перспективы выявления и освоения месторождений газа, конденсата и нефти на шельфе морей России (Сборник научных трудов), страница 40

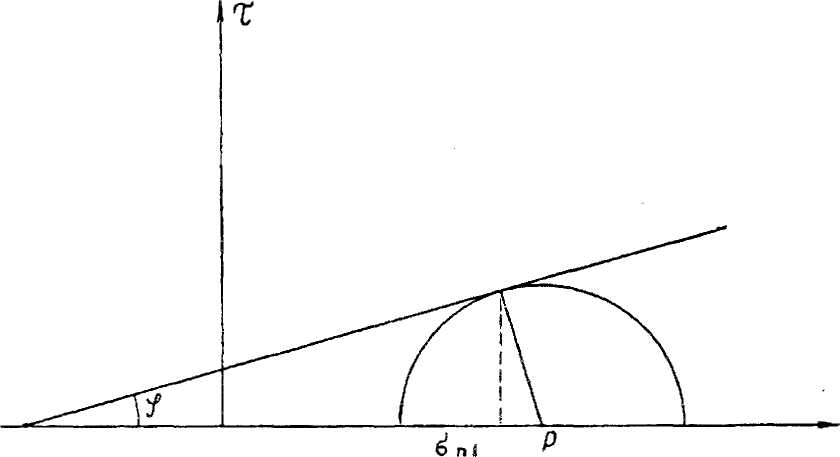
Общая схема к определению предельного сопротивления по лбу показана на рис. 6. Пусть давление но боковой поверхности имеет нормальную составляю игу ю р₀ и касательную т₀. К ней примыкает зо­на Ренкина, основной параметр который угол ц/. обусловленный со­отношением значений т₍₎ и р₀. К лобовой поверхности примыкает еще одна зона Ренкина стандартной, как в решении Прандля, конфигурации, определяемой углом // = — —.

4    2

Обе зоны Ренкина соединяются зоной, где линии скольжения -радиальные прямые R и логарифмитические спирали с начальной точкой 1 и конечной точкой 2. Для перехода от одной зоны Ренкина к другой воспользуемся уравнением Кеттера [4], которое для логариф­мической спирали принимает вид:

^-2г=0.                                           (3)

dx

Интегрируя данное выражение, имея в виду, что вдоль этой ли­нии касательные напряжения равны: t=a_ntg(p+c, получим решение от­носительно (т_п в виде:

^2{^          (4)

После некоторых преобразований получим выражение для удельного лобового сопротивления:

 ²^(5)

93

ливанию реализуется в виде контактных напряжений, распределен­ных по боковой поверхности с равнодействующей Qo и лбу с равно­действующей Q_jV Таким образом, полное усилие задавливанию Qo це­лесообразно представлять в виде суммы лобового сопротивления и сопротивления по боковой поверхности, т.е.

Oo=Q.,⁺Q₆-                                      (2)

Для определения лобового сопротивления воспользуемся мето­дами теории предельного равновесия, так как грунт под лбом в про­цессе погружения находится в предельном состоянии.

Общая схема к определению предельного сопротивления по лбу показана на рис. 6. Пусть давление по боковой поверхности имеет нормальную составляющую р_о и касательную т_о. К ней примыкает зо­на Ренкина, основной параметр который угол ij>, обусловленный со­отношением значений т_о и р_о. К лобовой поверхности примыкает еще одна зона Ренкина стандартной, как в решении Прандля, конфигура­ции, определяемой углом // = — - ^.

4   2

Обе зоны Ренкина соединяются зоной, где линии скольжения -радиальные прямые R и логарифмитические спирали с начальной точкой 1 и конечной точкой 2. Для перехода от одной зоны Ренкина к другой воспользуемся уравнением Кеттера [4], которое для логариф­мической спирали принимает вид;

^-2г = 0.                                      (3)

dx

Интегрируя данное выражение, имея в виду, что вдоль этой ли­нии касательные напряжения равны: T.=cr_ntg(p+c, получим решение от­носительно а_п в виде:

<т„ = -С - ctg(p + (<х,_; 1 + С ■ ctg(p)e^2(e-^a"^)!ga.                                                        (4)

После некоторых преобразований получим выражение для удельного лобового сопротивления:

q_n= -c-ctg^+ly'Vc-ctgSji)(1 +t_g5jTCtg^)e²^^dtg5;i,                                                              (5)

95

где 6_n - угол контактного трения, равный 5_я=ф-2; у\ Ф, с - нор­мативные характеристики грунта; ц=45-^\ &а = ~^ж-р-у/-^й* (в радианах); г-¹*",²*¹.

Зная удельное сопротивление, силы сопротивления задавлива-нию по лобовой поверхности предлагаем определять по зависимости:

Q^l-h-q,,                                         (6)

где / - длина ребра; b - длина поверхности.

Для расчета части нагрузки, которая воспринимается боковой поверхностью при задавливании ребра Q6, необходимо уметь опреде­лять две основные величины - нормальную составляющую давления на боковую поверхность и коэффициент грения грунта по боковой поверхности ребра tg5, используя общее выражение для Q6:

Q6=A|6sinP+(8+c-ctg<p) tgScosP],                                                             (7)

где А - площадь боковой поверхности; С - сцепление грунта; Ф - угол внутреннего трения грунта; р - угол раскрытия клина.