Нестационарные процессы в электрических цепях

НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

1. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

В радиотехнике, радиолокации, электрической связи, в системах и сетях передачи информации, автоматическом управлении и других областях техники основными проблемами являются получение, передача и обработка информации.

Термин «сигнал» часто встречается не только в областях науки и техники, но и в повседневной жизни. Не задумываясь о строгости, мы иногда отождествляем такие понятия, как сигнал, сообщение, информация. Занимаясь систематическим изучением теории электрических цепей (ТЭЦ), необходимо уточнить содержательный смысл понятия «сигнал».

Сигналом называется процесс изменения во времени физического состояния какого–либо объекта, служащий для отображения, регистрации и передачи сообщений.

Электрический сигнал – это изменяющееся во времени физическая величина (ток, эдс, напряжение, напряженность электрического или магнитного полей и т.д.), способная распространяться по проводам или в пространстве, в законе изменения которой содержится сообщение или информация.

1.1 СИГНАЛЫ И ФОРМЫ ИХ ПРЕДСТАВЛЕНИЯ

В связи с тем, что понятие «информация» наряду с материей и энергией принадлежит к фундаментальным философским категориям естествознания, то в курсе ТЭЦ не рассматривается вопрос о ценности информации, заключенного в нем сообщения и, в конечном счете, в сигнале.

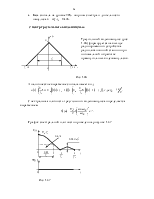
В процессе преобразования сообщения в электрический сигнал имеет место модуляция, т. е. управление параметрами некоторой электрической величины, называемой в дальнейшем модулирующей функцией. В результате модуляции соответствующий параметр становится функцией времени, а несущая функция превращается в сигнал. На рисунке 1.1 показан процесс формирования сигнала в модуляторе.

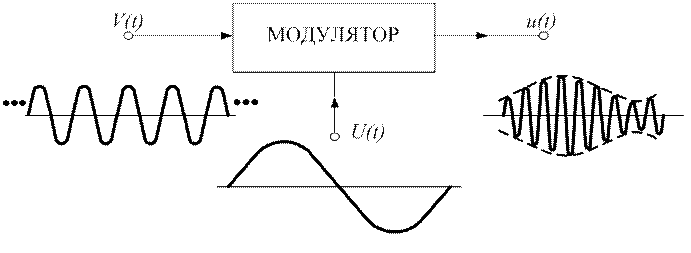
Рис. 1.1

Приняты следующие обозначения:

V(t) – несущий процесс, U(t) – модулирующая функция, u(t) – сигнал.

Классификация сигналов

В радиотехнике используют большое число различных сигналов. Для выявления общих свойств сигналов их классифицируют по ряду признаков.

·  По возможности предсказания мгновенных значений сигналов в любые моменты времени различают случайные и детерминированные сигналы.

Случайный сигнал представляет собой функцию времени, значения которой заранее неизвестны и могут быть предсказаны с вероятностью меньше единицы.

Детерминированный сигнал представляет собой функцию времени, все значения которой заранее известны или могут быть предсказаны с вероятностью равной единице.

В дальнейшем мы будем вести рассмотрение детерминированных сигналов и их прохождение через электрические цепи.

·  По величине интервала времени, в котором существуют отличные от нуля значения сигналов, различают непрерывные и импульсные сигналы.

·  По повторяемости мгновенных значений различают периодические и непериодические сигналы. Для периодических сигналов выполняется условие:

, где - период, - любое целое число.

К непериодическим сигналам относят одиночные и групповые (пачечные) сигналы.

·  В зависимости от выбора несущего процесса различают видеосигналы и радиосигналы.

Видеосигналы – это такие сигналы, у которых несущими процессами являются постоянные токи и напряжения.

Радиосигналы - это такие сигналы, у которых несущими процессами являются гармонические колебания и электромагнитные волны.

Кроме постоянных или синусоидальных токов и напряжений в качестве несущих процессов могут использоваться последовательности видеоимпульсов и радиоимпульсов.

Сигналы с такими несущими процессами являются импульсно-модулированными сигналами.

·  В зависимости от того, какой параметр несущего электромагнитного процесса подвергается модуляции, различают:

  амплитудно-модулированные радиосигналы (АМ),

  частотно- модулированные радиосигналы (ЧМ),

  фазомодулированные радиосигналы (ФМ),

  сигналы с модуляцией длительности импульсов,

  сигналы с модуляцией частоты следования импульсов,

  сигналы с модулированной модуляцией.

Сигналы во временной области. Типовые сигналы, применяемые в радиотехнике

Аналитическое или графическое представление сигналов как функций времени является представлением сигналов во временной области. С целью описания сигналов во временной области применяют элементарные сигналы: функцию включения и гармоническое колебание.

Рис. 1.2

Рис. 1.3

Рис. 1.4

                     Покажем на примерах, как типовые сигналы, применяемые в радиотехнике, могут быть описаны при помощи функций включения для видео – сигналов, для радио – сигналов, в качестве несущей функции необходимо использовать гармоническое колебание.

·  Одиночный прямоугольный видеоимпульс (рис. 1.5)

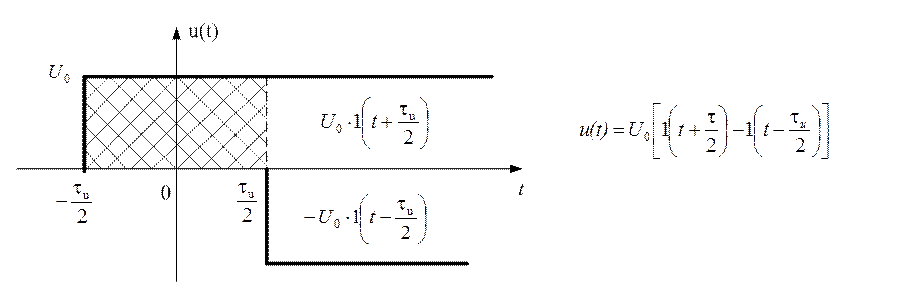
Рис. 1.5

·  Запаздывающий одиночный прямоугольный видеоимпульс (рис. 1.6)

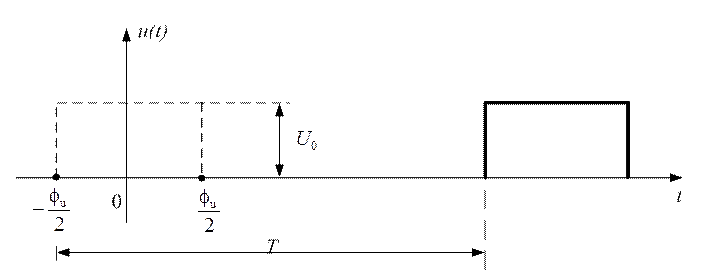
Рис. 1.6

Этот сигнал отличается от предыдущего тем, что элементарные функции включения задержаны на время Т, поэтому

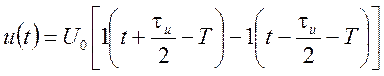
·  Описание импульсов прямоугольной формы, входящих в периодическую последовательность (рис. 1.7)

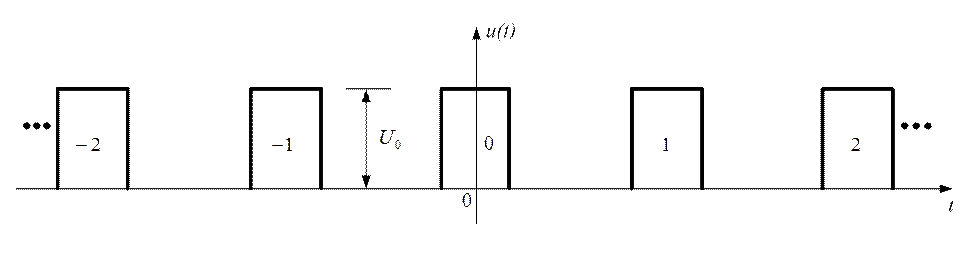
Рис. 1.7

Каждый импульс имеет свой номер (0, ±1, ±2, ±3, ..., ±К, ...).

Выше мы рассмотрели аналитическое описание «нулевого» импульса

,

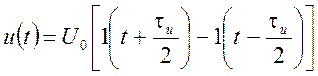и импульса запаздывающего на Т, т.е. первого импульса

,

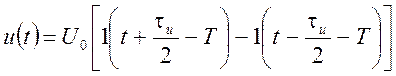аналогично можно записать выражения для второго импульса

,

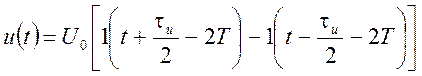и для импульса с номером К, где К=0, ±1, ±2, и т. д.

.

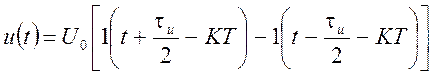·  Описание периодической последовательности прямоугольных

        видеоимпульсов

Так как периодическая последовательность является совокупностью импульсов с номерами К=0, ±1, ±2, и т. д. то аналитическое описание будет

.

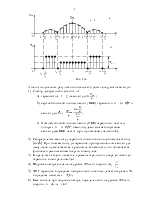
·  Описание прямоугольной пачки прямоугольных видеоимпульсов (рис. 1.8.)

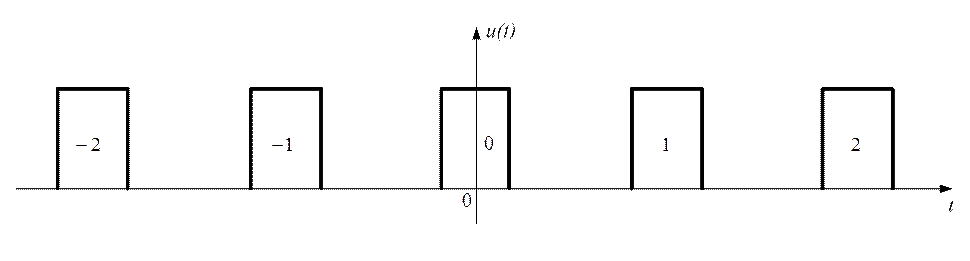
Рис. 1.8

Пачка состоит из пяти импульсов с номерами от –2 до 2. Аналитическое выражение для её описания будет

.

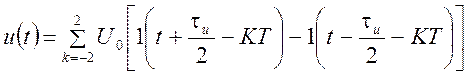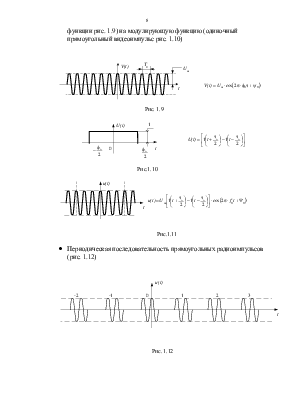
·  Одиночный прямоугольный радиоимпульс (рис. 1.11) может быть представлен как произведение несущего процесса (синусоидальной функции рис. 1.9) на модулирующую функцию (одиночный прямоугольный видеоимпульс рис. 1.10)

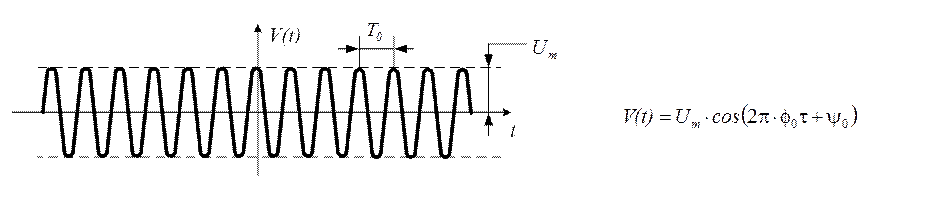Рис. 1.9

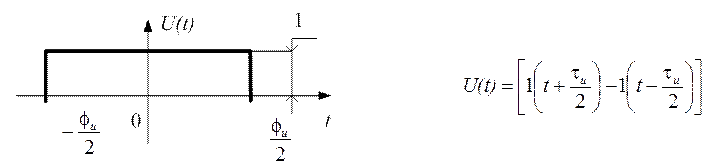
Рис.1.10

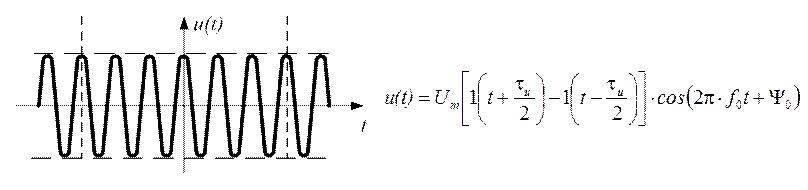
Рис.1.11

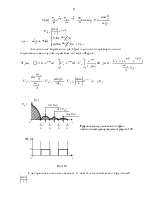
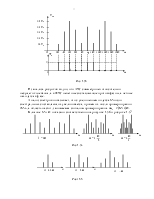
·  Периодическая последовательность прямоугольных радиоимпульсов (рис. 1.12)

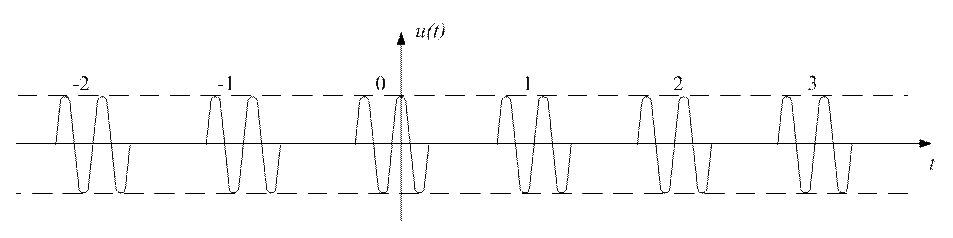
Рис. 1.12

.

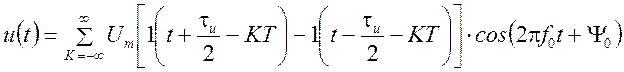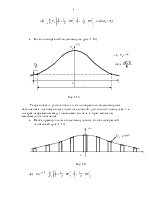
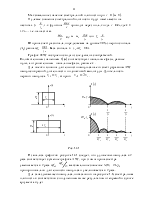
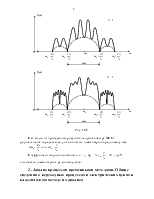
·  Колоколообразный видеоимпульс (рис. 1.13)

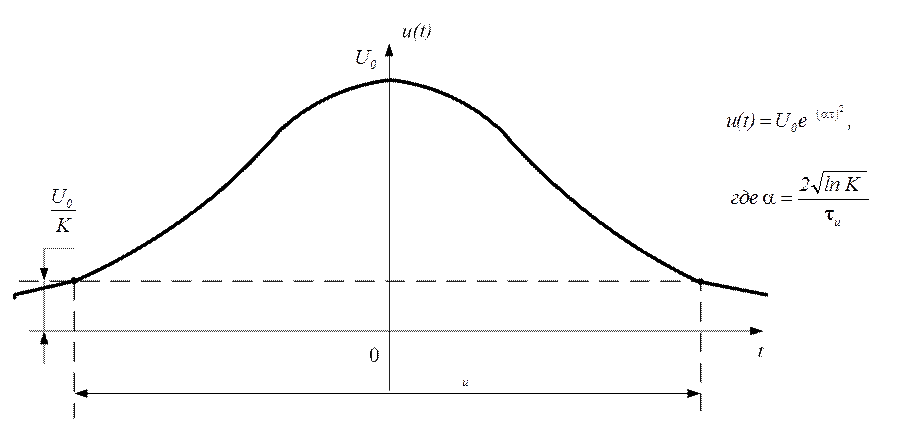
Рис. 1.13

Теоретически длительность колоколообразного видеоимпульса бесконечная, поэтому вводят понятие условной длительности импульса, т. е. интервала времени между значениями сигнала в раз меньшим максимального значения.

·  Пачка прямоугольных видеоимпульсов с колоколообразной огибающей (рис. 1.14)

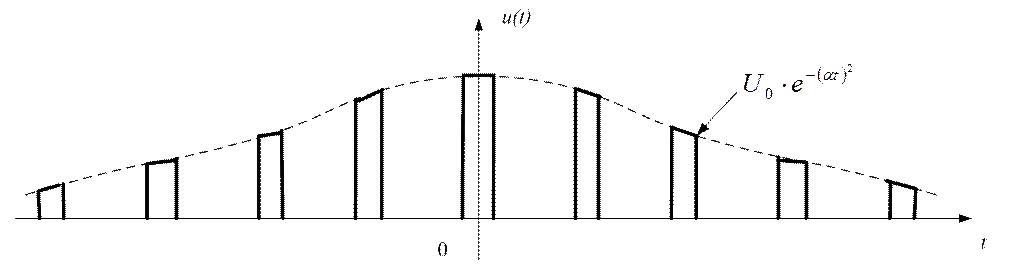
Рис. 1.14

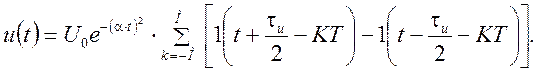
Согласно выражению, амплитуда каждого импульса изменяется в соответствии со значением огибающей колокольной формы.

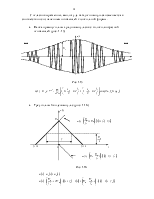
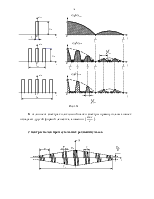
·  Пачка прямоугольных радиоимпульсов с колоколообразной огибающей (рис. 1.15)

 Рис. 1.15

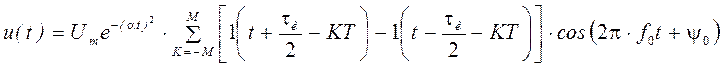
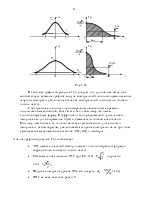
·  Треугольный видеоимпульс (рис. 1.16)

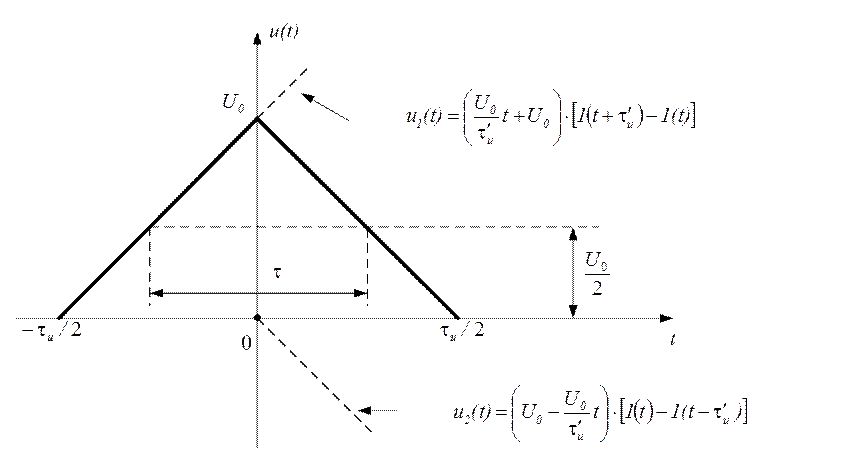
Рис. 1.16

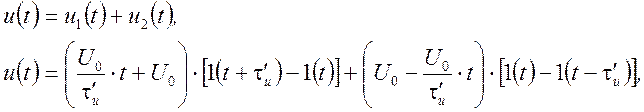
где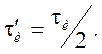

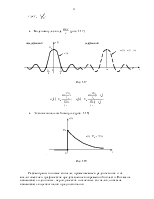
·  Видеоимпульс вида 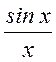 (рис. 1.17)

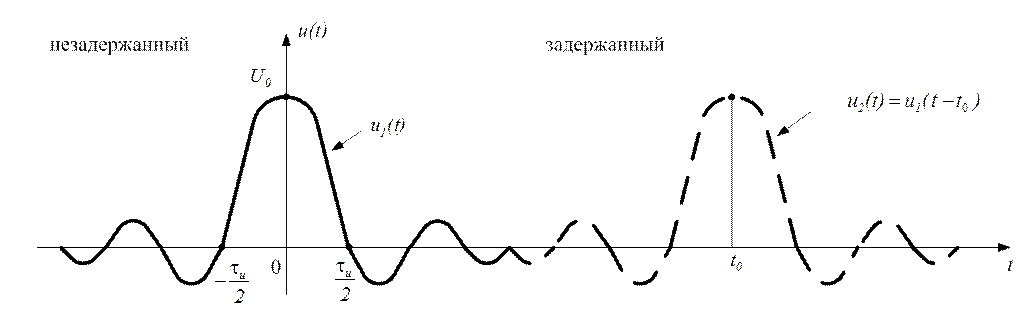
Рис. 1.17

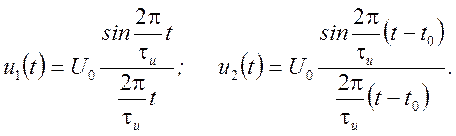
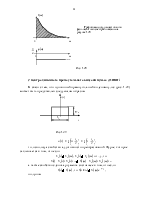
·  Экспоненциальный импульс (рис. 1.18)

.

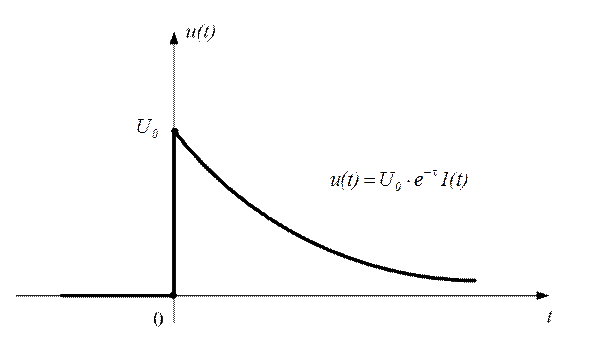
Рис. 1.18