Нестационарные процессы в электрических цепях, страница 24

Нелинейная индуктивность – это такой элемент, индуктивность которого зависит от величины протекающего тока. К таким элементам относят трансформаторы и катушки индуктивности с сердечниками из ферромагнитного материала, магнитный поток в которых зависит от величины тока в обмотке.

Нелинейные элементы в радиотехнических схемах условно обозначаются так:

Разделение элементов и цепей на линейные и нелинейные является чисто условным, поскольку реальные линейные элементы обладают некоторыми не линейными свойствами, а реальные нелинейные элементы обладают линейными свойствами в определенных пределах изменения напряжения или тока.

Свойства нелинейного сопротивления определяются вольт-амперной характеристикой (ВАХ).

Свойства нелинейных индуктивностей определяются вебер-амперной характеристикой.

Свойства нелинейных емкостей определяются вольт-кулонной характеристикой.

Примеры таких характеристик приведены на рисунке 5.1

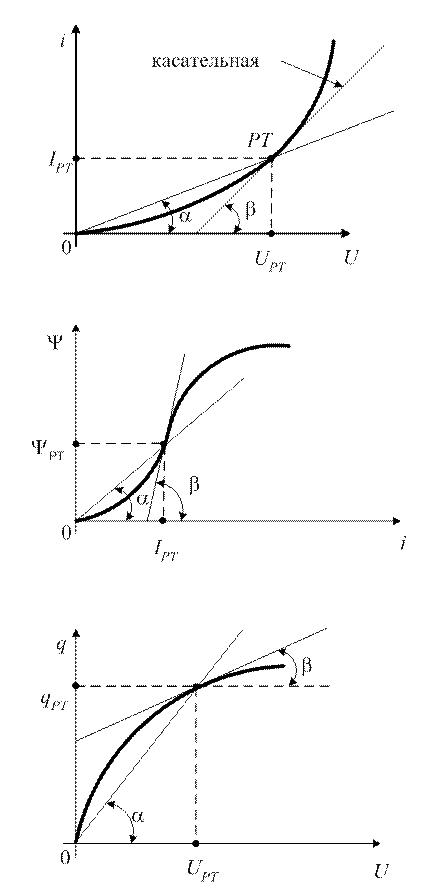
           Рис. 5.1

Для описания свойств нелинейных элементов используют статические (R₀, L₀, С₀) параметры и дифференциальные параметры (r_g, L_g, C_g).

Статические параметры используют при рассмотрении нелинейных цепей постоянного тока.

Дифференциальные параметры используют при рассмотрении нелинейных цепей переменного тока.

Статическими параметрами являются:

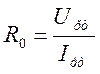- статическое сопротивление,

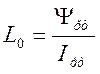 - статическая индуктивность,

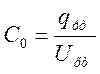 - статическая емкость.

Статические параметры нелинейных элементов зависят от выбранной рабочей точки (РТ). Статическое сопротивление определяет мощность потерь на нелинейном элементе в заданной рабочей точке

а статические емкость и индуктивность характеризуют запасную в них энергию

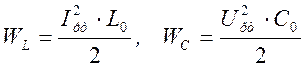
Дифференциальными параметрами являются:

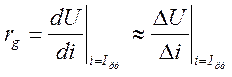 - дифференциальное сопротивление,

 - дифференциальная индуктивность,

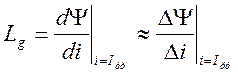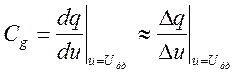 - дифференциальная емкость.

Дифференциальные параметры зависят от выбранной рабочей точки.

При небольших изменениях протекающих токов (приложенных напряжений) в окрестности выбранной рабочей точки нелинейных элементы можно считать практически линейными элементами, нелинейность которых проявляется лишь в том, что дифференциальные параметры зависят от управляющих токов (напряжений).

Свойства нелинейных цепей вытекают из рассмотренных ранее особенностей этих цепей.

·  Статические и дифференциальные параметры зависят от выбранного режима работы (рабочей точки).

·  Для нелинейных цепей принцип суперпозиции неприменим. Как видно из приведенного рисунка 5.2.

Если u1+u2=u3, то i1+i2≠i3

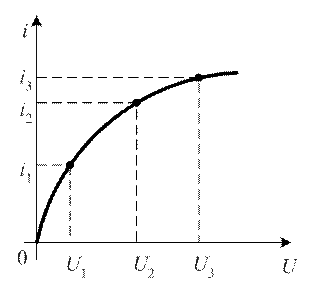
      Рис. 5.2

5.2. Аппроксимация характеристик нелинейных элементов

Обычно вольт-амперные (вебер-амперные, вольт-кулонные) характеристики определяются экспериментально и могут быть представлены в виде графика или таблицы. Между тем, для проведения расчетов необходимы аналитические зависимости. Такие аналитические зависимости приближенно определяют фактическую форму заданной характеристики, хотя приближение может быть весьма точным.

Аппроксимацией характеристик нелинейных элементов называют приближенное их представление аналитическими зависимостями.

Рассмотрим некоторые способы аппроксимации характеристик нелинейных элементов.

5.2.1. Кусочно-линейная аппроксимация

При кусочно-линейной аппроксимации заданная характеристика заменяется ломаной линией, составленной из прямолинейных отрезков.

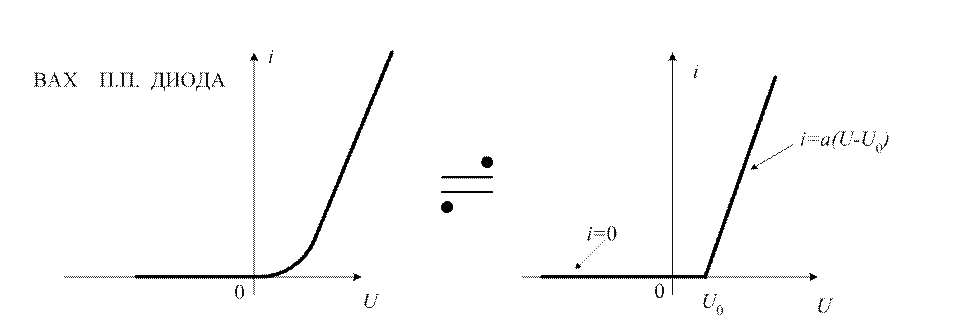
                            а)                                                      б)

Рис. 5.3

На рисунке 5.3 а (слева) показана реальные вольт-амперная характеристика полупроводникового диода. На рисунке 5.3 справа - приближенное представление этой характеристики отрезками прямой линии.

Аналитически заданную характеристику можно представить так

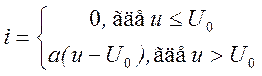
5.2.2. Аппроксимация степенным рядом

При этой аппроксимации заданная характеристика записывается в виде

где       х - независимая переменная,

y - зависимая переменная,

x₀ - рабочая точка,

a_k - коэффициенты аппроксимации.

Количество используемых членов ряда и их степени зависят от формы аппроксимируемой характеристики и от требуемой точности расчетов. Чем сложнее характеристика и чем выше требуемая точность расчетов, тем большее число членов ряда следует использовать.

Пример. Требуется определить аналитическое выражение, состоящее из трех членов ряда, аппроксимирующее анодно-сеточную характеристику лампового триода, если напряжение на сетке в рабочей точке равно U₀. Значения u₁, u₂, i₁, i₂, U₀, I₀ определяют из графиков (рис. 5.4) или таблиц, таким образом они являются известными. Для каждой из выбранных точек записывают аналитическое выражение и получают систему:

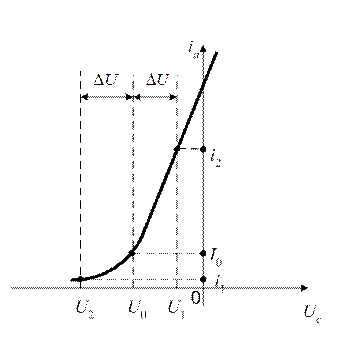
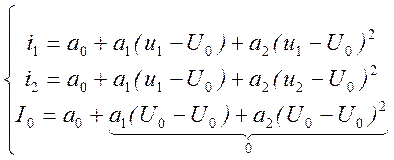
Рис. 5.4

Из данной системы коэффициент а₀ находят сразу:

а₀ = I₀ - его значение равно анодному току лампы в рабочей точке. Коэффициент  a₁ и a₂ находят, решая систему из двух уравнений с двумя неизвестными:

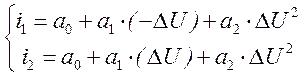
5.3. Понятие о методах расчета процессов нелинейных цепях

Расчет процессов в нелинейных цепях осуществляется с целью определения формы и спектра сигналов в нелинейных цепях.

5.3.1. Расчет формы отклика нелинейного сопротивления при воздействии синусоидальных колебаний

Пусть на нелинейное сопротивление (диод), с вольт-амперной характеристикой, приведенной на рисунке 5.5, подана синусоидальная э.д.с.

Через нелинейное сопротивление ток будет протекать лишь тогда, когда e(t)>U₀, именно в отрезки времени между моментами t₁ и t₂, а также  t₃ и t₄.

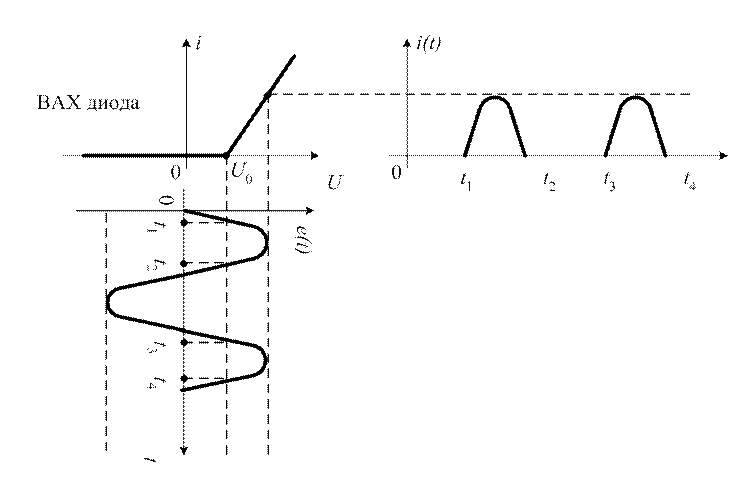
Рис. 5.5

Осуществляя подобные графические построения, несложно определить форму тока, протекающего через нелинейный элемент.