В случае воздействия на цепь синусоидального колебания отклик цепи определяется, как известно, с помощью комплексной передаточной функции, например:
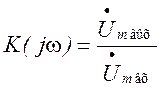, откуда 
Комплексная передаточная функция применима и для определения отклика цепи и на несинусоидальное воздействие, которое можно представить в виде суммы (или интеграла) комплексных амплитуд спектра (спектральной плотности).
3.1.1. Прохождение сигналов с дискретными спектрами
Пусть приложенное напряжение сложной формы можно представить в виде суммы ряда синусоидальных составляющих:
Для каждой спектральной составляющей можно записать
Как видно
Для определения спектральных составляющих отклика на выходе линейной цепи надо:
· амплитуды спектра входного сигнала умножить на соответствующие значения АЧХ цепи, в результате получим амплитуды спектра выходного сигнала;
· к начальным фазам входных спектральных составляющих прибавить соответствующие значения ФЧХ на заданных частотах, в результате получим начальные фазы спектральных составляющих выходного сигнала.
3.1.2. Если сигнал имеет сплошной спектр, то можно установить аналогичную связь между элементарными гармониками входного и выходного сигнала
,
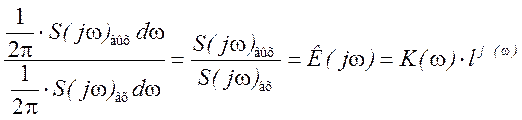где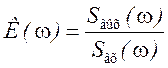 
- АЧХ цепи,
- ФЧХ цепи
Из этого следует, что для определения спектральной плотности сигнала на выходе необходимо, спектральную плотность сигнала на входе умножить на комплексную передаточную функцию.
3.2. Особенности передачи сигналов с дискретным спектром через линейные цепи
3.2.1. Прохождение сигнала с однотональной AM через настроенный колебательный контур
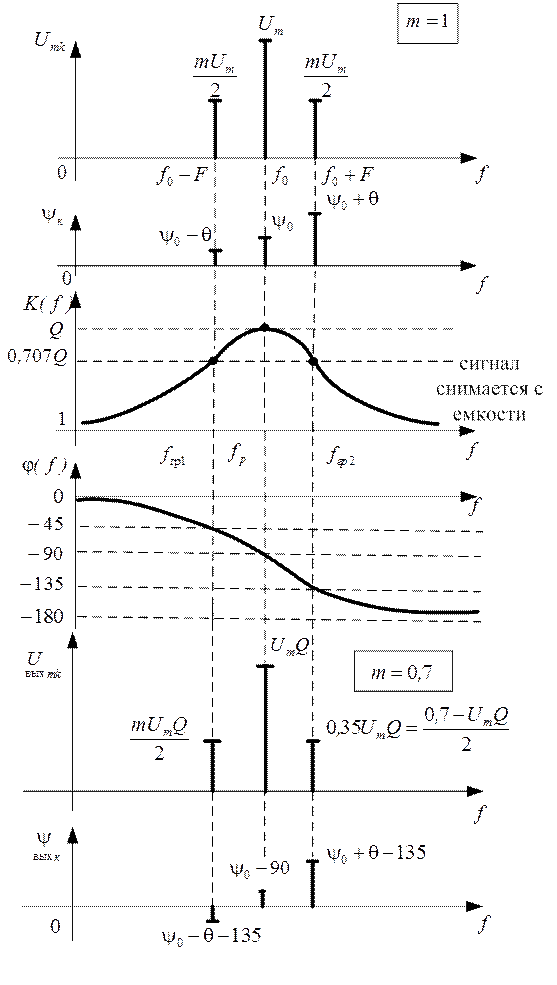
Спектры (АЧС и ФЧС) сигнала с однотональной AM приведены на рисунке 3.1.
АЧХ и ФЧХ колебательного контура, настроенного на несущую частоту сигнала, приведены ниже. Пусть частоты f0±F соответствуют граничным частотам полосы пропускания колебательного контура.
Перемножая амплитуды спектральных составляющих на соответствующие значения АЧХ и прибавляя к начальным фазам спектральных составляющих значения ФЧХ на соответствующих частотах, получим АЧС и ФЧС сигнала на выходе колебательного контура (рис. 3.1(внизу)).
Рис. 3.1
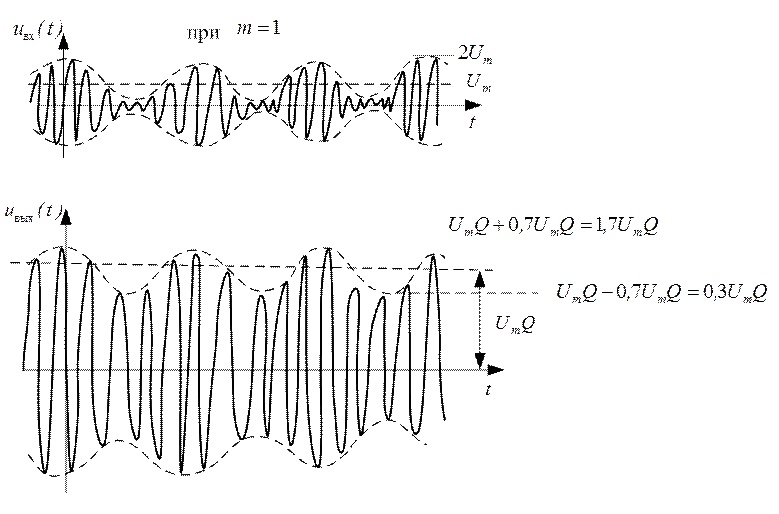
Рис. 3.2
Если контур обладает меньшей добротностью и, следовательно, большей полосой пропускания изменения формы и спектра сигнала будут меньше, чем в приведенном случае (рис. 3.2).
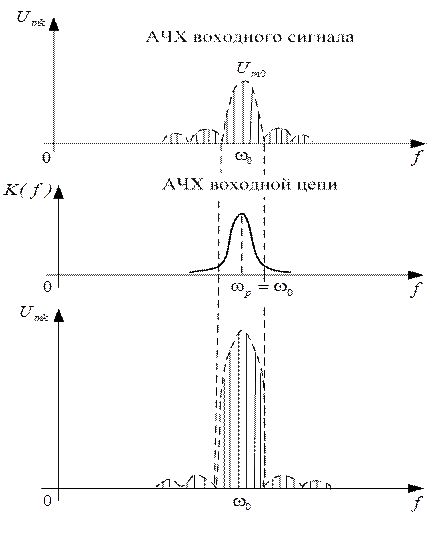3.2.2. Прохождение периодической последовательности
прямоугольных радиоимпульсов через настроенный колебательный контур
На практике очень необходимо знать, какие изменения спектра и формы сигнала будут иметь место при прохождении отраженных от цели импульсов через настроенный колебательный контур радио-приёмного устройства РЛС.
Как видно из приведенного рисунка 3.3, в результате прохождения совокупности спектральных составляющих через контур, имеет место изменение соотношения между амплитудами различных
спектральных составляющих, наибольшему «усилению» подверглись составляющие, близкие к резонансной частоте контура, остальные «усилились» в
Рис. 3.3 меньшей степени или даже уменьшились по амплитуде.
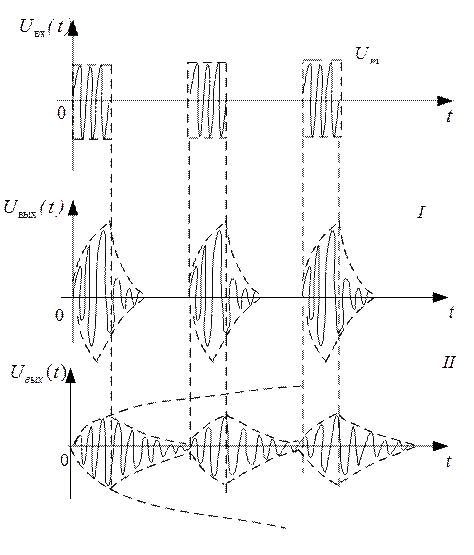
Если добротность контура невелика, то искажения формы имеют
место, как показано на рисунке 3.4(
), а при высокой
добротности процессы установления колебаний и затухания являются более длительным
(рис. 3.4()).
В случае более длительного входного импульса амплитуда могла нарастать до значения UmQ.
Анализируя график амплитудно-частотного спектра выходного сигнала можно сделать вывод о том в результате прохождения однотонального AM радиосигнала через настроенный колебательный контур, на выходе имеет место также однотонально-
Рис. 3.4
модулированный AM сигнал, однако амплитуда несущего колебания этого сигнала будет в Q раз больше амплитуды входного сигнала, кроме того, имеет место частичная демодуляция сигнала(фазовые изменения не рассматриваем.)
3.3. Понятие о квазистационарном методе
Квазистационарный метод анализа прохождения сигналов применяется в тех случаях, когда частота входного сигнала изменяется настолько медленно, что переходные процессы, возникающие при изменении частоты, протекают значительно быстрее, чем происходит сколько-нибудь заметное изменение частоты. Рассмотрим ряд примеров, нашедших широкое применение на практике.
3.3.1. Прохождение радиосигнала с однотональной угловой модуляцией через колебательный контур
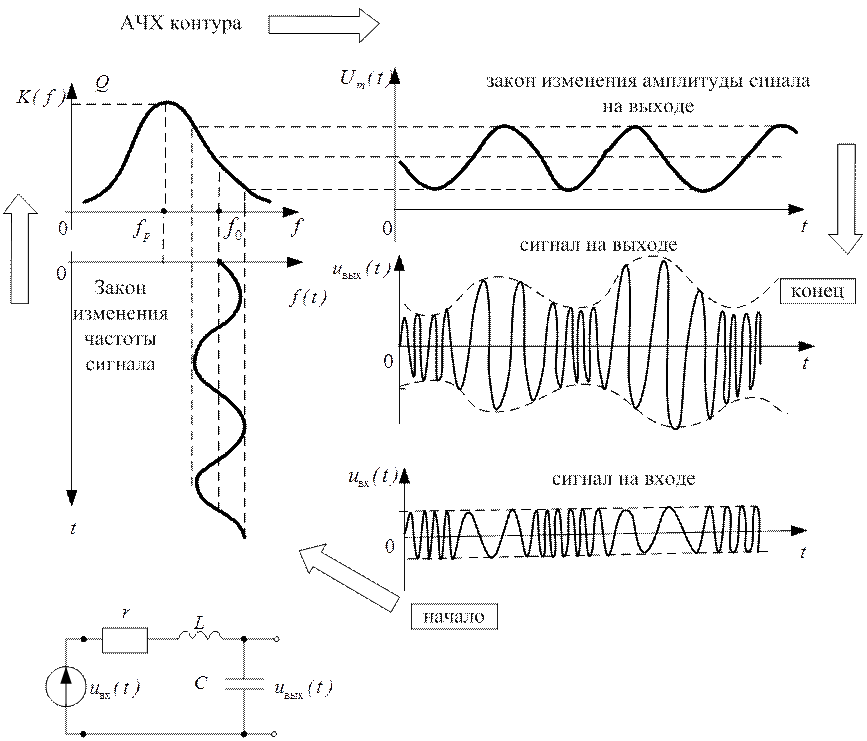
Рис. 3.5
Как видно из рисунка 3.5, резонансная частота контура не совпадает с несущим колебанием сигнала на входе. Область частот, в пределах которых изменяется частота входного сигнала лежит на «скате» АЧХ контура. В результате того, что частота входного сигнала медленно меняется по синусоидальному закону, амплитуда выходного напряжения на ёмкости также будет изменяться по синусоидальному сигналу, выходной сигнал будет иметь в отличие от входного не только угловую, но и амплитудную модуляцию.
Рассмотрев данный вопрос, мы разобрали принцип работы частотного дискриминатора, который применяется в радиотехнике с целью выделения закона угловой (частотной) модуляции из радиосигнала с УМ (ИМ), такие дискриминаторы применяются при приеме сигналов УКВ ЧМ радиовещания.
3.3.2. Прохождение радиосигнала с ЛЧМ через электрические цепи
Рассмотрим пример прохождения радиосигнала с ЛЧМ через систему связанных колебательных контуров при связи больше критической.
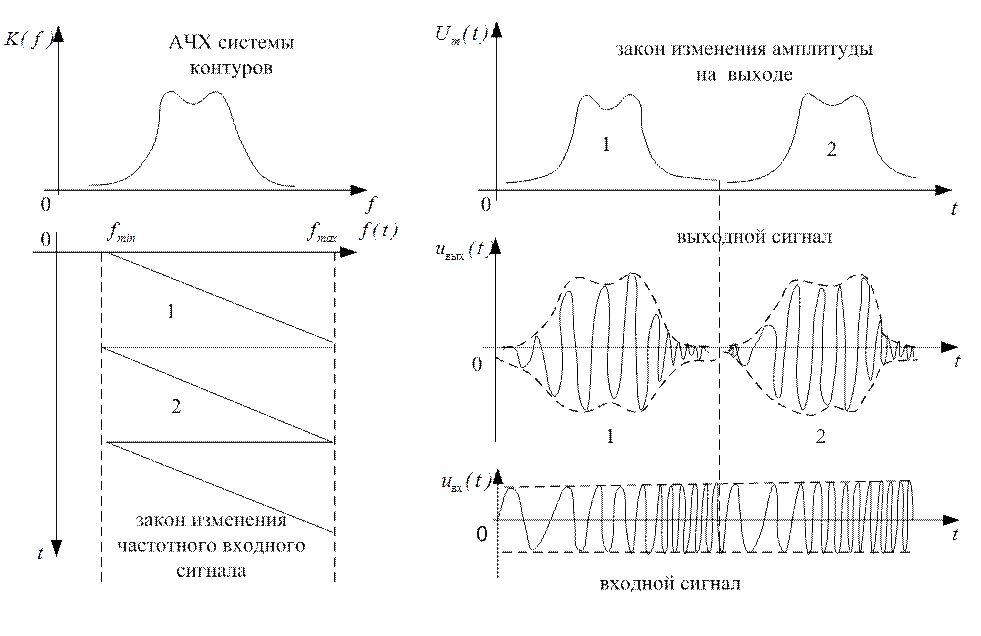
Рис. 3.6
Из графиков (рис. 3.6) видно, что частота входного сигнала медленно нарастает по линейному закону от fmin до fmax, затем частота резко уменьшается до fmin и цикл повторяется вновь. Амплитуда входного сигнала постоянна.
По мере изменения частоты сигнала амплитуда на выходе будет изменяться в соответствии с законом изменения АЧХ, т.к.
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.