|
№ |
СИГНАЛЫ НА ВХОДЕ |
СИГНАЛЫ НА ВЫХОДЕ |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
Приведенные в таблице выражения являются следствием свойства линейности электрических цепей.
Связь между переходной G(t) и импульсной H(t) характеристиками выражается следующими двумя выражениями:
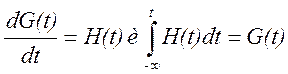
Расчет временных характеристик электрических цепей разделяют, как правило, на два этапа:
определение переходной характеристики цепи G(t) классическим методом расчета;
определение импульсной характеристики цепи H(t) путем дифференцирования переходной характеристики.
Пример: Переходной характеристикой цепи, изображенной на рисунке 2.52, является аналитическое выражение:
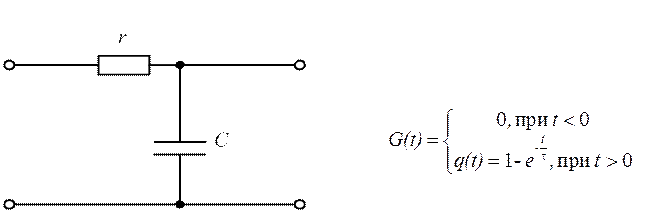
Рис. 2.52
Другой формой записи функции G(t) является:
![]() ,
,
эта форма записи подчеркивает тот факт, что переходная характеристика определена для t > 0. Здесь q(t) функция, определенная, для всех моментов времени.
Действительно, если построить график функции 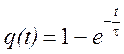 (рис. 2.53) из которого видно, что
при t < 0 имеют место некоторые значения функции q(t),
однако, с физической точки зрения, до подачи единичной ступенчатой функции 1(t) в цепи были
нулевые начальные условия. Поэтому аналитическое выражение переходной
характеристики цепи должно быть следующим:
(рис. 2.53) из которого видно, что
при t < 0 имеют место некоторые значения функции q(t),
однако, с физической точки зрения, до подачи единичной ступенчатой функции 1(t) в цепи были
нулевые начальные условия. Поэтому аналитическое выражение переходной
характеристики цепи должно быть следующим:
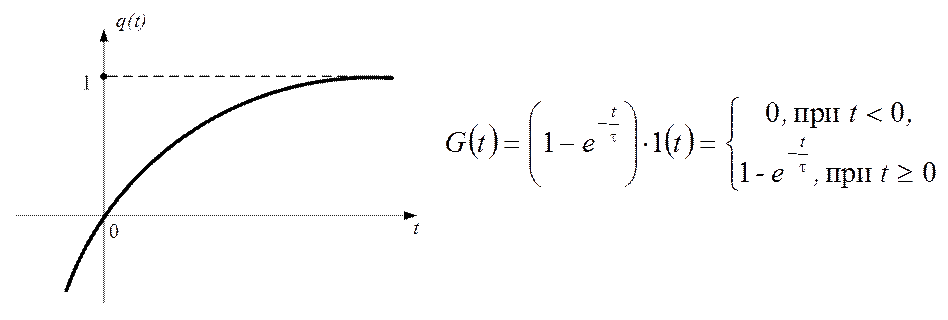
Рис. 2.53
Импульсная характеристика любой электрической цепи может быть рассчитана исходя из соотношения:
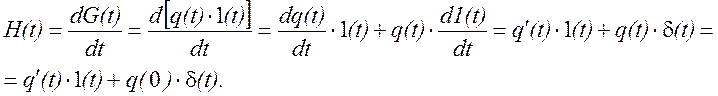
Определим импульсную характеристику цепи, изображенной на стр.89
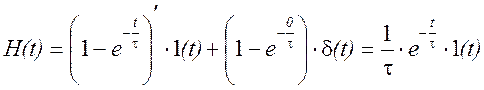
![]() Второе
слагаемое данного выражения равно нулю, т.к. в момент существования
Второе
слагаемое данного выражения равно нулю, т.к. в момент существования ![]() - функции значение q(t)=0.
- функции значение q(t)=0.
2.9.4. Представление произвольных сигналов при помощи типовых воздействий
С помощью одиночных ступенчатых функций(скачков) можно
описать широкий класс сигналов. Например, для описания прямоугольного импульса
с амплитудой Е и длительностью ![]() следует применить
два скачка (рис. 2.54):
следует применить
два скачка (рис. 2.54):
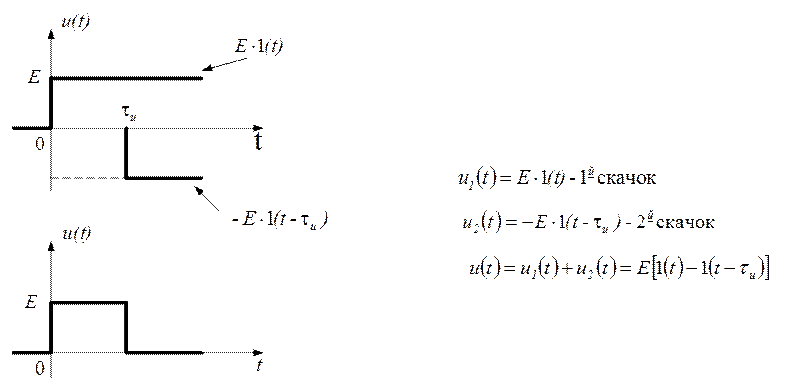
Рис. 2.54
Если сигнал изменяется непрерывно по произвольному закону с разрывом при t=0, то его можно произвольно заменить ступенчатым воздействием, как это представлено на рисунке 2.55.
Если просуммировать все скачки, то получим приближенное равенство:
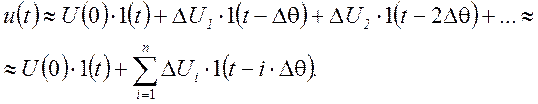
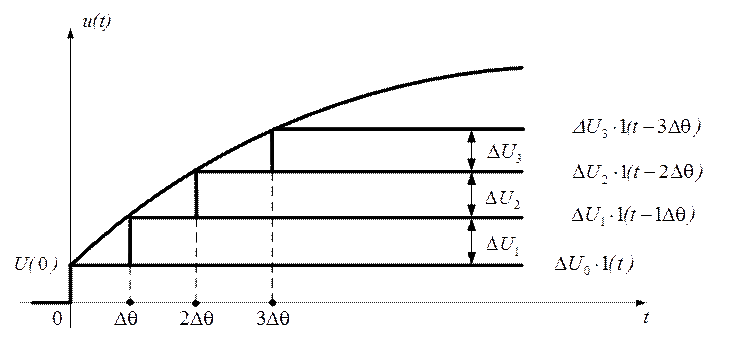
Рис. 2.55
Представление произвольного сигнала при помощи суммы
скачков будет тем точнее, чем меньше отрезок времени ![]() .
.
Разделив и умножив полученное выражение на ![]() , и устремив
, и устремив ![]() к
нулю, получим:
к
нулю, получим:
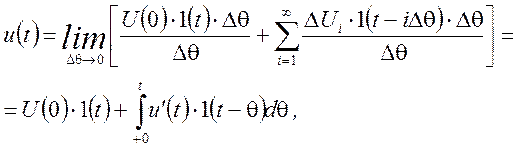
где 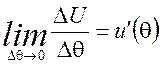 - производная
сигнала в произвольный момент времени
- производная
сигнала в произвольный момент времени ![]() .
.
Для случая, когда в первоначальный момент времени t=0 скачок отсутствует и значение сигнала равно нулю, аналитическое выражение будет (рис. 2.56):

Рис. 2.56
С помощью ![]() - функции также
можно представить любые произвольные сигналы. На рисунке показано, что сигнал
произвольной формы может быть примерно представлен в виде совокупности
прямоугольных импульсов малой длительности (рис. 2.57):
- функции также
можно представить любые произвольные сигналы. На рисунке показано, что сигнал
произвольной формы может быть примерно представлен в виде совокупности
прямоугольных импульсов малой длительности (рис. 2.57):
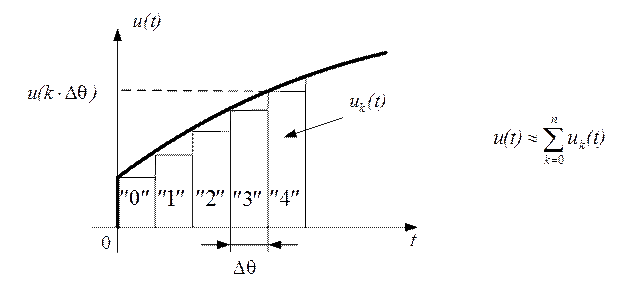
Рис. 2.57
где ![]() - аналитическое
выражение короткого прямоугольного импульса с номером k.
- аналитическое
выражение короткого прямоугольного импульса с номером k.
Определим предел выражения:
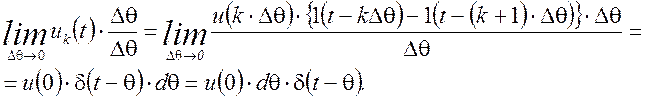
Из этого выражения видно, что очень короткий прямоугольный
импульс (элементарный импульс) длительностью ![]() может
быть представлен произведением его площади
может
быть представлен произведением его площади ![]() на
на
![]() - функцию в момент существования
этого импульса.
- функцию в момент существования
этого импульса.
Сигнал произвольной формы может быть представлен бесконечной суммы(интеграла) элементарных импульсов:
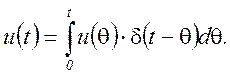
2.9.5. Определение реакции цепи на произвольное воздействие по переходной и импульсной характеристикам
В приведенной в п. 2.9.3. таблице, показана связь между сигналами на входе и на выходе цепи, являющаяся следствием свойства линейности электрических цепей.
Действительно, если сигнал на входе цепи:
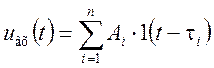
и на выходе
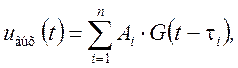
то для произвольного сигнала
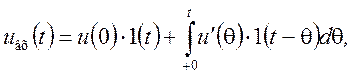
аналогично можно записать
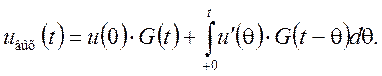
Полученное выражение носит название интеграла Дюамеля. Алгоритм расчета сигнала на выходе цепи при помощи интеграла Дюамеля с переходной характеристикой:
Для заданной цепи определяют переходную характеристику G(t).
Определяют функции, входящие в состав интеграла Дюамеля:
а) находят ![]() путем замены в
формуле G(t) переменной t на
путем замены в
формуле G(t) переменной t на ![]() ;
;
б) находят ![]() путем
дифференцирования заданного сигнала
путем
дифференцирования заданного сигнала ![]() по времени с
последующей заменой переменной t
на
по времени с
последующей заменой переменной t
на ![]() .
.
Подставляют полученные выражения в формулу интеграла
Дюамеля, интегрируют по переменной ![]() и при
необходимости подставляют пределы интегрирования.
и при
необходимости подставляют пределы интегрирования.
Показано, что если входной сигнал может быть представлен в виде бесконечной суммы(интеграла) скачков, то сигнал на выходе может быть представлен в виде бесконечной суммы(интеграла) откликов на эти скачки.
Путем аналогичных рассуждений можно показать, что если входной сигнал может быть представлен в виде бесконечной суммы (интеграла) элементарных импульсов:
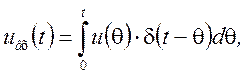
то сигнал на выходе цепи, импульсная характеристика
которой ![]() также может быть представлен в виде
бесконечной суммы (интеграла) откликов на эти элементарные импульсы:
также может быть представлен в виде
бесконечной суммы (интеграла) откликов на эти элементарные импульсы:
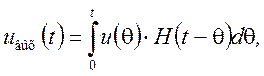
Алгоритм расчета сигнала на выходе цепи при помощи интеграла Дюамеля с импульсной характеристикой.
1. Для заданной цепи определяют
импульсную характеристику ![]() .
.
2. Определяют величины входящие в интеграл Дюамеля:
а) заменяя в выражении для ![]() переменную
переменную ![]() на
на
![]() получают
получают ![]() ;
;
б) заменяя в выражении ![]() переменную
переменную ![]() на
на
![]() получают
получают
![]() .
.
3. Подставляют полученные
выражения в формулу интеграла Дюамеля, интегрируют по переменной ![]() и,
при необходимости, подставляют пределы.
и,
при необходимости, подставляют пределы.
2.9.6. Другие способы представления произвольных сигналов
Имеется целый ряд элементарных функций,
кроме ![]() и
и ![]() при
помощи которых можно аналитически описать любое произвольное воздействие.
при
помощи которых можно аналитически описать любое произвольное воздействие.
· Применение функций вида 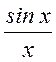 -
теорема Котельникова.
-
теорема Котельникова.
Если имеется некоторый сигнал ![]() который не претерпевает скачков или
других резких изменений на интервале времени
который не претерпевает скачков или
других резких изменений на интервале времени ![]() ,
то такой сигнал может быть представлен в виде разложения в ряд:
,
то такой сигнал может быть представлен в виде разложения в ряд:
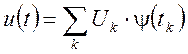 ,
,
где ![]() - значение
функции
- значение
функции ![]() в равностоящие моменты времени:
в равностоящие моменты времени:
![]()
![]() -
интервал дискретизации;
-
интервал дискретизации;
![]() -
элементарные функции вида
-
элементарные функции вида 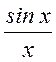 , сдвинутые между
собой на время
, сдвинутые между
собой на время ![]()
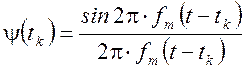 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.